1. 概要: Post-hoc test とは
   • 実例
   • 早見表
2. Post-hoc test としての多重比較検定
   • Bonferroni test
   • Fisher's LSD test
   • Tukey, Tukey-Kramer test
   • Newman-Keuls test
   • Duncan's multiple range test
   • Dunnett's test

群間比較の基本である t 検定を例に、仮説検定の考え方を解説しています。以下の順番に読んでみて下さい。

1. 仮説検定
2. z 検定
3. t 検定の原理 - 母平均の検定
4. 対応のある t 検定
5. t 検定 メインページ: 等分散の場合
6. Welch の t 検定: 分散が同じと言えない場合
7. Mann-Whitney の U 検定: ノンパラメトリックな二群比較
8. t 分布
9. 実践: Excel での t 検定, 平均値と分散を用いた t 検定

概要: Post-hoc test とは

一般に、群が複数ある場合には、次のような手順で統計検定を行う。事後検定 post-hoc test とは、通常 ANOVA ののちに行われる多重比較の群間検定の総称である。

1. Shapiro test などの正規性の検定を行う。
2. 正規分布 が仮定できる場合には、ANOVA を行う。
3. ANOVA の結果が有意だった場合、どの群の間で有意差があるかどうかを調べるために、post-hoc test を行う。

post-hoc は、"after this" を意味するラテン語である。

Dunnet, Tukey-Kramer, Bonferroni は F 統計量を用いない多重比較であるため、ANOVA で有意でなくても有意差が出ることがある (3)。これらについては、前もって ANOVA をかける必要がない。

一方、Scheffe, Games/Howell, Fisher PLSD は F 統計量を用いているため、前もって ANOVA をかける必要があり、ANOVA で有意でなければ有意差は出ない (3)。

実例

いくつか ANOVA と post-hoc test の実例を示しておく。データは 棒グラフ で示されることも多いが、最近では以下のような情報量が多いグラフが好まれる。

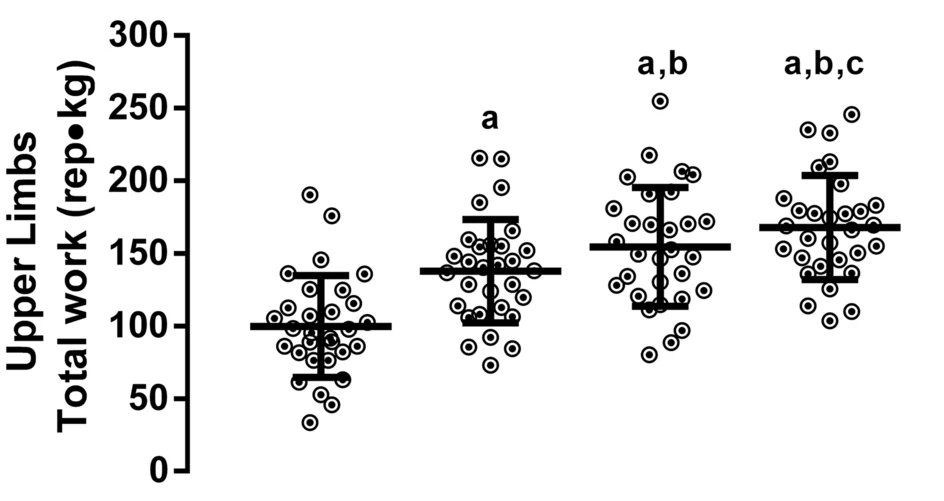
文献 5 より。ANOVA (repeated measures) と Tukey's post-hoc test が使われている。

早見表

文献 2, 7 などから。リンクはページ下の詳しい説明に飛びます。

Post-hoc test としての多重比較検定

文献 7 に、1960 - 2019 の間に生態学の論文で使われた post-hoc test の集計が載っている。基準が厳しい Bonferroni が一番人気で、次いで Tukey HSD となる。

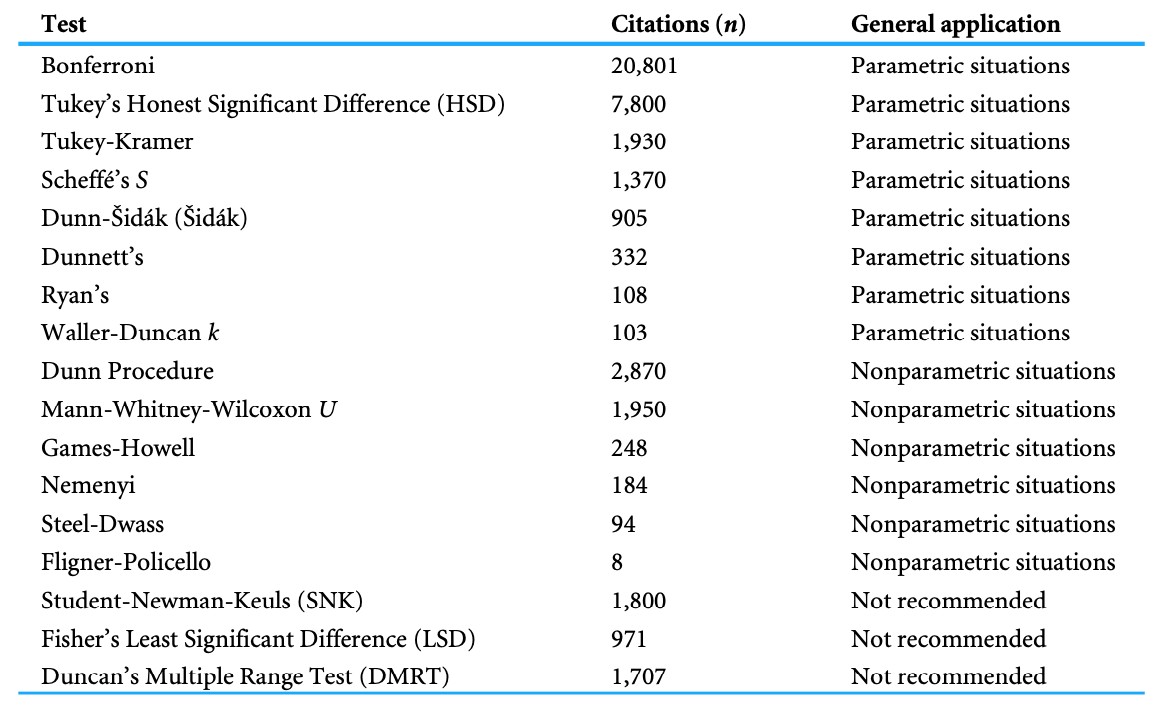
非推奨となっているのは、主に type I error の確率の高さによる。この図も文献 7 から。LSD と Duncan' MRT のエラー率が突出しており、SNK でもかなり高いことがわかる。

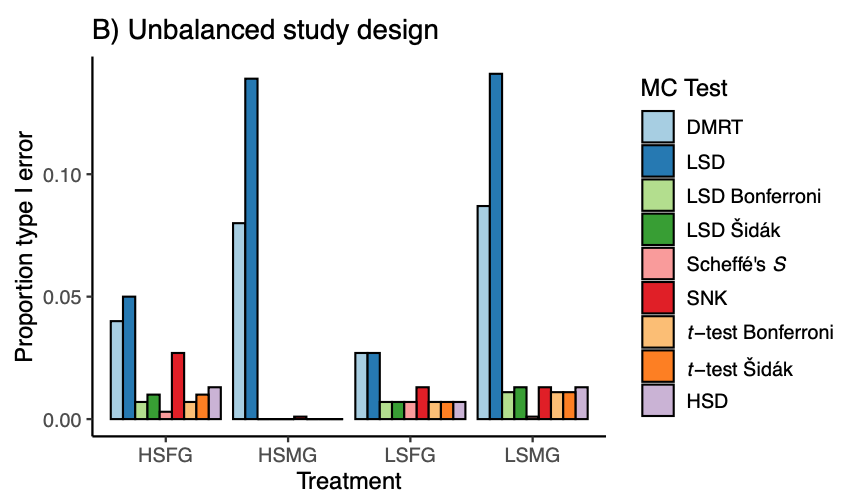
HSFG = high sample size with few groups; HSMG = high sample size with many groups, LSFG = low sample size with few groups; LSMG = low sample size with many groups

ボンフェローニの検定

Bonferroni test は検定の多重性を調整する方法のひとつで、有意水準を直接いじる 最もわかりやすい方法である (3)。正規分布、等分散を仮定。

• 3 群で仮説を検定する場合、2 群の組み合わせの検定を 3 回繰り返す必要がある。このときには、有意水準 0.05 を 3 で割って 0.017 とする。
• 同様に、4 群の場合は 6 回の検定が必要なので、0.05/6 = 0.0083 を有意水準とする。

群が増えると有意水準がどんどん低くなり、厳しくなりすぎるという問題がある。5 群以上の検定では用いるべきではないとされているが、この点を改良したのが Holm 法、Shaffer 法である (3)。

Fisher's LSD

LSD は least significant difference の略。文献 3 では、多重性の問題が考慮されておらず 3 群のみに限定される と書かれている (3)。また、この Prism という統計ソフトの マニュアル の記述がわかりやすい。英語なので簡単に意訳しておく。

• Fisher's LSD は、基本的には t 検定のセットであり、ANOVA の follow up のみに使われる。t 検定との違いは、t 検定では 2 群の pooled SD を使うが、Fisher's LSD では全ての群の pooled SD を計算する点である。
• Bonferroni, Tukey, Dunnett and Holm とは異なり、多重性の補正を行わない。この方法を使う場合は、データ解釈などで多重性の問題を考慮しなければならない。

Tukey および Tukey-Kramer 法

日本語では、Tukey はテューキーまたはチューキーと表記されることが多い。Tukey 法は各群の n が揃っている場合しか使えないので、現在ではこの方法の発展であるチューキー・クレーマー検定 Tukey-Kramer test がよく使われる。

Tukey-Kramer 法は、各群の n が同じでも違っていても使うことができる (3)。Tukey HSD (honestly significant difference) 法と呼ばれることもあるが、両者は同じ検定である。

Newman-Keuls test (SNK)

日本語では「ニューマン = コイルス法」である。Student-Newman-Keuls と書かれることもある。

Tukey-Kramer よりも検出力が高いが、第一種の過誤を起こしやすい。

ダンカンの多重比較検定

Duncan's multiple range test は Newman-Keuls を発展させて作られた検定である。

Wikipedia には 「Duncan's new multiple range test (MRT) などとも呼ばれる多重比較法。第 1 種の過誤 type I error のリスクを高めることを許容し、第 2 種の過誤 type II error に対して堅牢 protective な検定である」とあるが、文献 3,4 では 多重性の問題を考慮していないため使用すべきではない と書かれている。

なぜ多重性の問題を考慮していないと言われるかは、文献 4 で詳しく解説されている。英語では少し異なる表現がされているようで、type I error を意図的に増やして Newman-Keuls の問題点を解決しようとしていると書かれているページもあった (引用していたがリンク切れ)。

"Duncan's MRT does not control family wise error rate at the nominal alpha level, a problem it inherits from Student–Newman–Keuls method. The increased power of Duncan's MRT over Newman–Keuls comes from intentionally raising the alpha levels (Type I error rate) in each step of the Newman–Keuls procedure and not from any real improvement on the SNK method."

Dunnett's test

対照群とその他の比較に用いる。

References

1. 山中ら 2009a. 分子生物学、生化学、細胞生物学における統計のポイント. 蛋白質核酸酵素 53, 1792-1801.
2. 私のための統計処理. Link.
3. 池田 2013a. 統計検定を理解せずに使っている人のために III. 化学と生物 51, 483-495.
4. 山村 1998a. 土壌肥料学における数理統計手法の応用上の問題点. 3. Duncanの多重検定はなぜ使えないか. 日本土壌肥料学会誌、69, 649-653, 1998.
5. Correa et al., 2020a. Resistance training improves sleep quality, redox balance and inflammatory profile in maintenance hemodialysis patients: a randomized controlled trial. Sci Rep 10, 11708.
6. 対馬, 統計的検定資料1 多重比較法. 弘前大学 医学部 保健学科 理学療法学専攻.
7. Midway et al., 2020a. Comparing multiple comparisons: practical guidance for choosing the best multiple comparisons test. PeerJ 8, e10387.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。

↑