内容が増えてきたら独自のページを作っています。多くの項目は、このページに簡単なサマリーがあり、詳細をリンク先の別のページで説明しています。

1. 検定方法の選び方
2. 連続型データの検定 (2 群の場合)
3. 連続型データの検定 (3 群の場合)
4. 事前検定の是非
5. 標準化されたデータに対する t 検定

検定方法の選び方

このページでは、以下のフローチャートに従って、データの種類に応じて検定方法を決定する手順を紹介する。

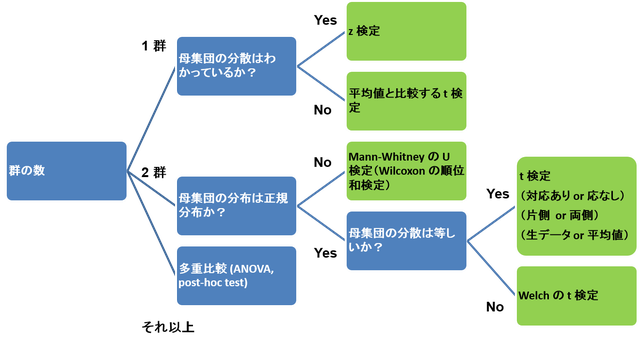
フローチャート以前に、まずデータが離散型か連続型かを判断する必要がある。離散型のデータとは、例えば以下のようなもの。

• A さんと B さんが今まで食ったパンの枚数を比較する。
• 組織切片で免疫染色を行い、染まった細胞の数を A 群と B 群で比較する。
• A 群と B 群にストレスを与え、生き残った個体数を比較する。

これらのデータは整数以外の値を取らない。したがって分布は正規分布にはならず、離散型の分布になる。このようなデータには、正規分布を仮定する t 検定を適用することはできず、ノンパラメトリックな Mann-Whiteney の U 検定 や カイ二乗検定を使う必要がある。詳細は 計数データの検定 のページへ。

データが連続型であるなら、次の判断基準は群の数である。

1 群 の検定で、平均値がある値に等しいかどうかを知りたい場合には、z 検定 や 平均値と比較する t 検定 が使われる。

2 群 の場合には、母集団の分布が問題となる。母集団が特定の分布に従うことを仮定した検定をパラメトリック検定と呼び、そうでないものをノンパラメトリック検定という。このページにある「連続型データの検定 (2 群の場合)」へ進む。

3 群 以上の場合は、多重検定を行うことになる。上の表にはパラメトリックな多重検定である ANOVA およびその post-hoc テスト のみが示されている。

連続型データの検定 (2 群の場合)

以下の手順がよく用いられている。フローチャートも再掲しておく。

1. まず、Shapiro-Wilk 検定 でデータが正規分布に従うかどうかを調べる (参考: R による Shapiro-Wilk 検定)。
2. 正規分布に従わない場合は、ノンパラメトリックな 2 群の検定、Mann-Whitney の U 検定 を用いる。
3. 正規分布に従っている場合、次に 2 群が等分散であるかどうかを調べる。F 検定。
4. 分散が異なる場合は Welch の t 検定 を用いる。
5. 分散が等しい場合、データが対応しているかどうかに応じて 対応のある t 検定 または 対応のない t 検定 を用いる。

ただし、この手順に従うと、一つのデータセットに対して Shapiro-Wilk 検定、F 検定、t 検定など、複数回の統計処理を行うことになる。これは多重検定という問題を生じる。「事前検定の問題」を参照。

連続型データの検定 (3 群の場合)

3 群以上の場合も、基本的な手順は同じである。

1. まず、Shapiro-Wilk 検定 でデータが正規分布に従うかどうかを調べる。
2. 正規分布に従わない場合は、ノンパラメトリックな 3 群以上の検定、Kruskal-Wallis 検定を行う。これで有意ならば、群間比較を Steel-Dwass などのノンパラメトリック post-hoc test をする。
3. 正規分布に従っている場合、パラメトリックな ANOVA を適用するが、その前に等分散の検定を行う。3 群以上の等分散性の検定には、R のバートレット検定が便利である (参考)。
4. 分散が異なる場合は、対数変換などの措置をとるか、ノンパラメトリック検定を用いる (参考)。Games-Howell が等分散性を仮定しない post-hoc test である。
5. 分散が等しい場合、Tukey HSD などの等分散性を仮定した post-hoc test をする。

詳細は 多重検定のページ を参照のこと。

事前検定の問題

問題は以下の 2 点である。正規性を例に説明しているが、等分散性を事前検定する場合でも全く同じである。

1. 最初に正規性の検定を行い、確認できたら t 検定。この手順を踏むと、同じデータに対して 2 回統計をかける ことになる。これは 2 重検定であり、基本的に避けるべき。全体の有意水準が 5% に収まらなくなる。
2. 正規性の検定における 帰無仮説 は、「正規分布する」である (8)。この仮説が棄却できない場合、「正規分布する」として t 検定をすることになるが、この状態は論理的に「正規分布するという仮説を棄却する証拠が不十分である」ということで、「正規分布する」ことを証明してはいない。したがって「正規分布するために t 検定をした」という論理に正当性がない。

私は、基本的には事前検定には反対で、最初からノンパラメトリックなテストを行うべきという立場である。この点については、事前検定の是非 で解決法を含めて検討している。

標準化されたデータに対する t 検定

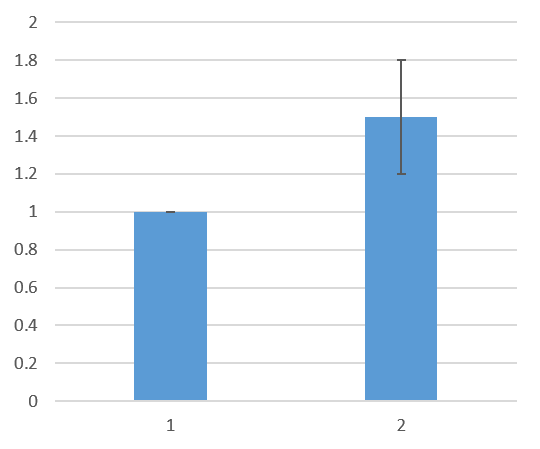
図のように、コントロール群の値が全て 1 でエラーバーがなく、実験群の値だけにエラーバーがついている図を見たことがあるだろうか。

このようなデータに対して t 検定をかけるのは誤りであると考えている。詳細は 標準化されたデータに対する t 検定 のページにまとめた。

References

1. 山中ら 2009a. 分子生物学、生化学、細胞生物学における統計のポイント. 蛋白質核酸酵素 53, 1792-1801.
2. Gronke et al. 2010a. Molecular evolution and functional characterization of Drosophila insulin-like peptides. PLoS Genet 6, e1000857.
3. t検定をばかにしてはいけない。の巻き。 Link: Last access 2018/06/03.
4. Kawada et al. 2013a. High concentrations of L-ascorbic acid specifically inhibit the growth of human leukemic cells via downregulation of HIF-1a transcription. PLoS ONE 8, e62717.
5. Okumura's Blog; 2 段階 t 検定の是非. Link: Last access 2018/06/03.
6. 統計勉強: 等分散性の検定について. Web.
7. Welch検定が主流、単純 t 検定や ANOVA は時代遅れ：Statwingの話題から. Link.
8. Rochon et al. 2012a. To test or not to test: Preliminary assessment of normality when comparing two independent samples. BMC Med Red Method 12, 81.
9. Square Root Transformation. Link: Last access 2018/07/20.
10. ポストホックテストとしての多重比較検定. Link: Last access 2022/05/01.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。