1. 概要: z 検定とは
2. 例題 1: 平均価格がいくらであると言えるか？
   • 仮説の設定
   • z 値の計算
   • z 値の分布
   • MATLAB でさらに解析

概要: z 検定とは

z 検定とは z 値を検定統計量とする仮説検定 hypothesis test であり、母集団 parent population の 分散 が既知の場合 に、標本集団の平均値がある数と等しいかどうかを評価することができる (1)。

ただし、実際の生物学実験では 基本的に母集団の分散は未知 であり、z 検定を使う場合はほとんどない。例えば普通のマウスを使った生物学実験では、世の中の全てのマウスが母集団である。

z 検定の考え方は t 検定と非常によく似ているので、このページは t 検定 を勉強する前のトレーニングのようなものと認識するのが良いだろう。

例題 1: 平均価格がいくらであると言えるか？

仮説の設定

仮説検定のページ の流れに従い、

帰無仮説: 平均価格は 117 円である。
対立仮説: 平均価格は 117 円ではない。

のように仮説を設定する。

z 値の計算

さらに、検定統計量 z を下のように定義する。m は標本平均、μ は母平均、σ は母標準偏差、n は標本数である。

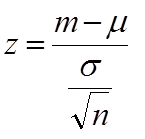
なお、t 値との違いは母集団の標準偏差 σ を用いるか標本集団の不偏分散の標準偏差 u を用いるかだけである。

上の 20 個の値から計算すると、z = -2.7578 となる。そこで次に、この -2.7578 という値が現れる確率がどれだけ小さいかを検討することになる。

z 値の分布

この z 値は、標準正規分布に従う統計量である。したがって、このサイト などにある標準正規分布表や、以下の標準正規分布の図 (Public domain; σ=1 とおく) から求めることができる。

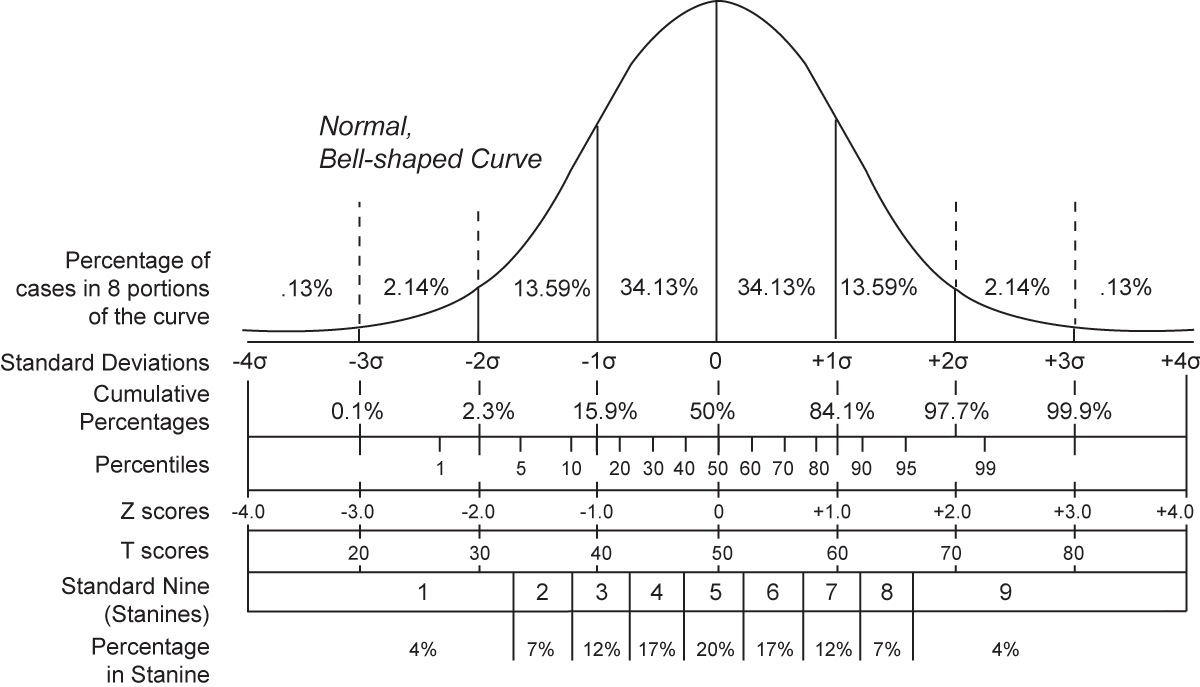
Z score の -2.7578 は、Cumulative % が 2.3% と 0.1% の間、やや 1% 寄りである。つまり このような z 値 が得られる確率は非常に小さい。ゆえに帰無仮説「平均価格 = 117」は棄却され、「平均価格は 117 円であるとは言えない」という結論になる。

文献 1 には、正規分布表のかわりに MATLAB の normimv 関数を使う方法が説明されている。2.5% の片側確率を与える z 値は、1.9600 および -1.9600 である。また、z = -2.7578 に対応する p 値は normcdf 関数で求めることができ、両側で 0.0058 となる。

MATLAB でさらに解析

上の結果を、MATLAB で実際に z 値の分布を見ながら再解析してみよう。やっていることは

• この地域に、スーパーマーケットが全部で 100 軒あると仮定し、卵の平均価格を 117 円、標準偏差を 3 円とする。
• 上の問題のように無作為に 20 軒を選び、z 値を算出する。このステップを 1 回行う試行 trial、2 回繰り返す試行、・・・ 5000 回繰り返す試行を行う。
• 実際に 1.96 より大きい z と -1.96 より小さい z が出現する割合を計算してみる。繰り返し数が多くなれば、0.05 に近づいていくはずである。

結果

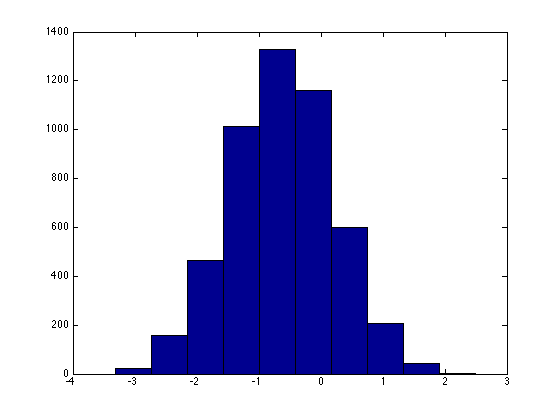
z 値の分布。それぞれの trial について 1 個の z 値を記録してヒストグラムにした。

一応、標準正規分布に近い形になっているが、中心が微妙にずれている。おそらく、トータル 5000 回では十分でないのだろう。t 分布のページ で計算した t 値も、理想に近い分布になるまでに 100,000 個の値が必要だった。

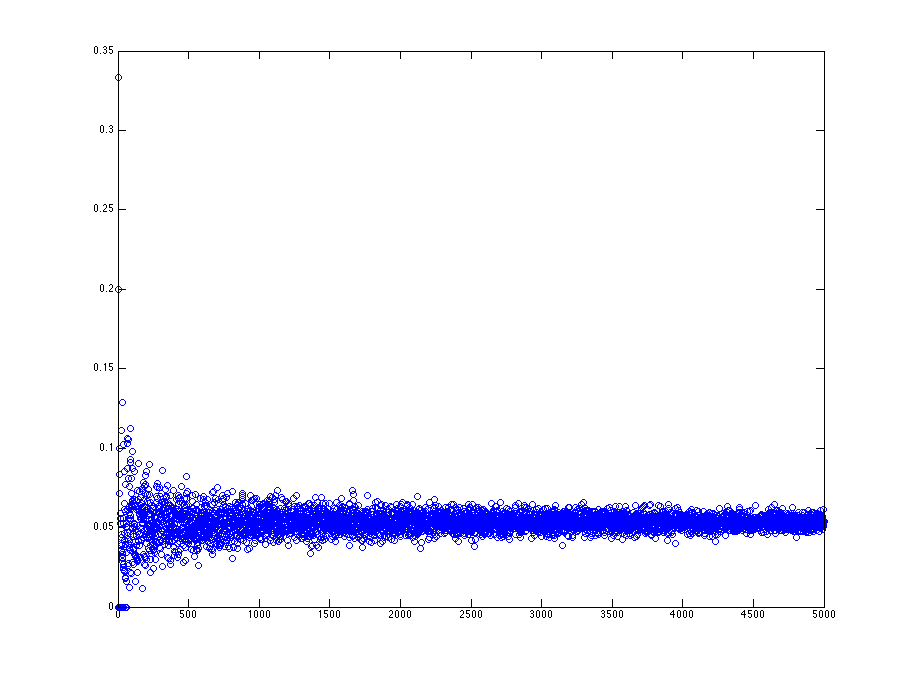
横軸に繰り返しの回数、縦軸に 1.96 より大きい z と -1.96 より小さい z が出現する割合をプロットした。500 回程度の繰り返しでは、z の出現割合 (要するに P 値) は 0.25 - 0.75 ぐらいの範囲になるが、繰り返しが増えると 0.05 に収束している。

References

1. MATLAB による仮説検定の基礎. Web pdf.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。

アップデート前、このページには以下のようなコメントを頂いていました。ありがとうございました。2018 年 11 月 11 日に訂正しました。