1. 概要: t 検定とは
2. 対応のない等分散 t 検定の原理
3. R による対応のない等分散 t 検定

概要: t 検定とは

t 検定とは、t 分布に従う 検定統計量 t を利用する検定法 の総称である。一般に、2 組のグループ (標本集団) があるとき、それらの集団のもつ値の平均値が有意に異なるかどうかという検定に用いられるが、以下のように様々なパターンがある。

1. ある標本集団 (1 群) の母集団の平均値が特定の値に等しいかどうか
2. 2 群の母集団の平均値が等しいかどうか
3. 回帰直線を引いたときに、その勾配が 0 に等しいかどうか

いずれの場合も、「帰無仮説 = 等しい、対立仮説 = 等しくない」である。

このページでは、「対応がなく 分散 が等しいと仮定できる場合の t 検定の原理」 と、t 検定を使う際の実践的な注意事項を解説する。t 検定について原理からよく理解したい人は、以下の順にページを読んでもらいたい。

1. 仮説検定
2. z 検定
3. t 検定の原理 #1: 母平均の検定
4. t 検定の原理 #2: 対応のある t 検定
5. t 検定の原理 #3: 正規分布、等分散の場合: このページ
6. Welch の t 検定: 等分散を仮定できない場合
7. Mann-Whitney の U 検定: 正規分布 を仮定できない場合。ノンパラ。
8. 実践 1: Excel での t 検定

対応のない等分散 t 検定の原理

分散が等しいと仮定できる場合は、対応のある t 検定とほとんど状況が変わらない。 唯一異なるのは、標本数が等しいとは限らない ので、検定統計量を定義する際にこの点を考慮しなければならないことである。この問題は、併合分散 merged variance と呼ばれる分散値を使うことで解決する。

母分散の値はわからないが、2 標本の分散が等しいと仮定できるので、それらをプールした併合分散を考えることができる。

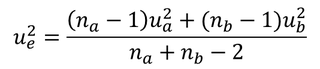
u²_e は併合分散、u²_a は 標本 A の分散、u²_b は標本 B の分散、n_a は A の標本数、n_b は B の標本数である。

ここで以下のように検定統計量 t を定義すると、これは自由度 n_a + n_b -2 の t 分布に従う。

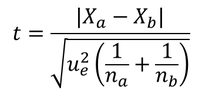
X_a, X_b は、それぞれの標本の平均値である。 あとはこの通りに t を算出し、通常の仮説検定を行えばよい。

ここのポイントは、等分散を仮定すると併合分散を導入できることである。等分散を仮定できない場合は、以上の操作を近似に基づいて行う Welch の検定が必要になる。「概要」の項目から、Welch の検定へ進むこと。

等分散性の検定

また、等分散性の検定をかけてから平均値の比較を行っている場合もあるが、この是非については Preliminary test のページ を参照のこと。

R による対応のない等分散 t 検定

更新予定、とりあえずコマンドのみ。

• t.test(group1, group2, var.equal=T) で等分散を仮定した検定
• t.test(group1, group2, var.equal=T, paired=F) で paired
• t.test(group1, group2) で Welch の検定

References

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。