分散: 定義、意味、計算方法など

UB3/statistics/basics/variance

このページの最終更新日: 2024/09/30

定義: いろいろな分散

分散 variance にはいくつか種類がある。

母分散 population variance
標本分散 sample variance
不偏分散 unbiased variance (or unbiased estimate of variance, unbiased estimate of population variance)

母集団の分散のこと。m 個のデータ (x₁, x₂, x₃, ... x_m-1, x_m) から成る母集団があり、X をその平均としたとき、母分散 σ² は

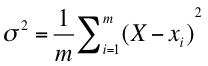
と表される。なお、X - x_iを偏差 deviation という。

母分散は記述統計 descriptive statistics ではよく使われる値であるが、推測統計 inferative statistics を使うような生物学実験では、母集団についてのデータを得ることはできない (参考)。

このような場合、標本集団である実験群から得られたデータの分散は、次に示す標本分散 sample variation である。そして、いかに標本分散から母分散を推定するかということを考える必要が出てくる。

n 個のデータ (x₁, x₂, x₃, ... x_n-1, x_n) から成る標本集団があり、X をその平均としたとき、標本分散 s² は

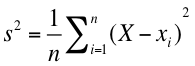
である。 Sample variation なので、s² で表されることが多い。

つまり、全ての要素について平均値からのずれ (偏差) を2乗し、その平均をとったもので、式の形は母分散と同じである。母集団についてデータを得ることができないので、この標本分散から母集団を推定することになる。

ただし、一般に使われるのは以下に示す不偏分散であり、標準偏差 standard deviation も不偏分散から求めるのが普通である。

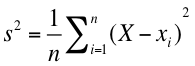
詳細はよくわからないが、上記の標本分散 sample variance は、母分散の推定値にはならないことが統計学的に証明されている。そこで、母分散と同じ期待値をもつ以下の不偏分散 unbiased variance が使われる。形の上では、単に n を n - 1 にしただけである。

Unbiased variation なので、u² と表されることが多い。しかし、u を表す決まった言葉はないようで、

などのような多様な表記がある (3)。単に標準偏差と書いてある場合は、n ではなく n-1 を使ったこちらの分散の平方根を意味する。

Excel の関数 =stdev も不偏分散であり、分母に n をおきたい場合は =stdevp を用いる (Excel Mac 2011 で確認) 。

ここで、なぜ n でなく n-1 を使うのかという点について、長崎大学情報データ科学部高橋将宜氏の以下のような主旨のツイートがあった。

非常に大きな母集団から 1 つをサンプリングすると、そのデータがそのまま標本集団のデータとなり、この場合、標本分散はゼロになる。
標本分散は母分散の推定に使うことができる。しかし、標本分散 = 0 のとき、母分散は 0 と推定される。これは不可能ではないが、n = 1 のとき、母分散を常に 0 と推定してしまうことになる。
ゆえに、n = 1 による分散の算出 (= 母分散の推定) には意味がない。
データが最低 2 つあれば、標本分散を計算でき、そこから母分散の推定が可能になる。これは、1 人目の情報を使わず、2 人目のデータのみから情報を得ていると考える (n - 1 で、一人分の情報を使っているとする)。ゆえに分母には n - 1 が使われる。

分散 σ² はバラツキを表す指標であるが、2 乗しているために平均値と次元が異なる。そこで、分散の平方根である標準偏差 σ もよく使われる。

分散では偏差を 2 乗するので、標準偏差に比べて、平均との差が大きく評価される。

分散の計算式には、平均値が使われる。したがって、平均値に意味のあるようなデータで、分散はより大きな意味をもつと言える。「平均値に意味のあるデータ」の詳細は、平均値のページを参照のこと。ここでは簡単に述べる。

平均値および分散は、そのデータの分布が正規分布に近いとき、ばらつきの指標として大きな意味をもつ。

図 (Public domain) は平均 0、分散 = 標準偏差 = 1 の正規分布 (標準正規分布) である。分散および標準偏差が大きいと、潰れたような形のべたっとした分布になる。

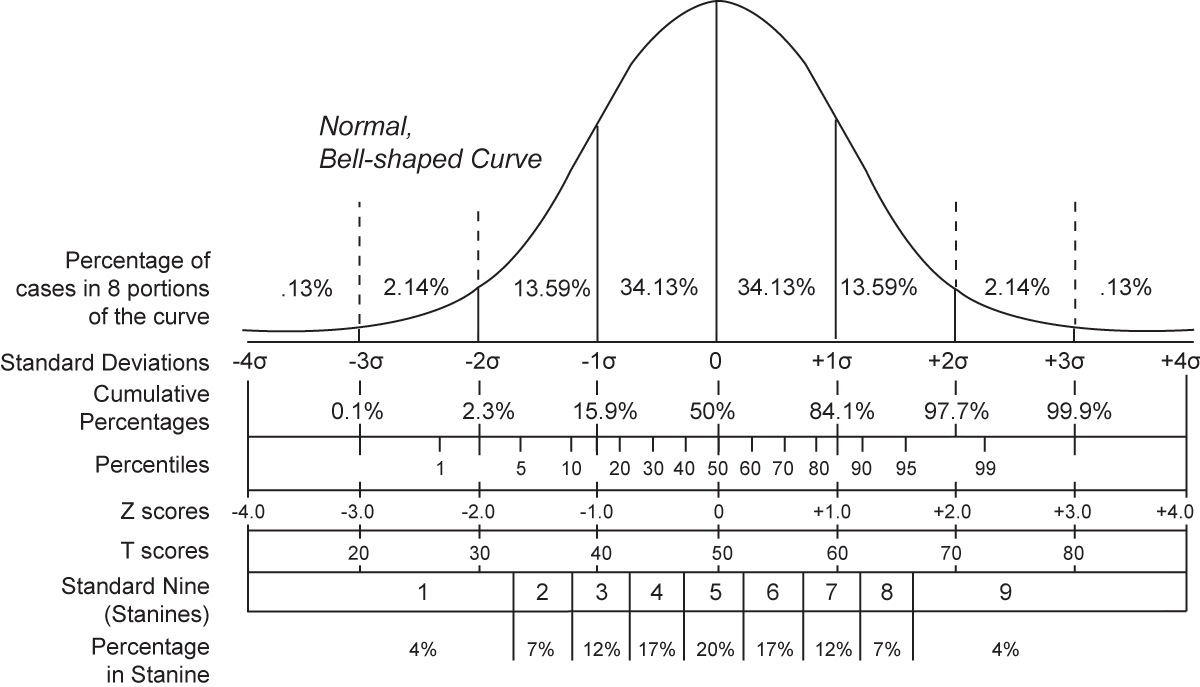
一方で、こちらの図 (Public domain) のような二峰性 (2 つのピークがあるという意味) の分布では、分散や標準偏差という概念があまり意味がないことがわかる。

Excel の関数 =stdev は、分母に n ではなく n - 1 を置いた不偏標準偏差である。n を使う場合は =stdevp を用いる。 (Excel Mac 2011 で確認)

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。