仮説検定: 原理、帰無仮説、対立仮説など
UB3/statistics/basics/hypothesis
このページの最終更新日: 2025/11/23- 概要: 仮説検定とは
広告
概要: 仮説検定とは
仮説検定とは、母集団に関して立てた
- 仮説を設定する
- 検定統計量を求める
- 判断基準を定める
- 仮説を判定する
なぜ、わざわざ否定するための仮説を立ててから、それを否定するという面倒な形をとるのかは、ページ下方の「白鳥の例え」を参考にすると分かりやすい。
1. 仮説を設定する
検定を行う人は、2 つの仮説、
帰無仮説は、主に
- 喫煙者と非喫煙では、体重に差がない。両者の体重をそれぞれ BwS および BwNS と置くと、BwS = BwNS。
- ある地域のスーパーマーケットの昨年の卵 1 パックの平均価格は 117 円であった。今年の平均価格 m も同じく 117 円である (1)。 (m = 117)
対立仮説は、帰無仮説と背反関係 (同時に成り立たないということ) にある仮説のことをいう。上の帰無仮説と対応して、
- まず考えられるのは、BwS ≠ BWNS である。
しかし、BwS > BWNS や BwS < BWNS も帰無仮説と背反関係にあり、対立仮説として用いることができる。つまり、可能な対立仮説は- BwS ≠ BWNS。これは「BwS > BWNS または BwS < BWNS」と同等である。
- BwS > BWNS
- BwS < BWNS
両側検定 、下の 2 つのうちいずれかの仮説を用いる検定を片側検定 という。 - 同じ論理により、m ≠ 117, m > 117, m < 117 の 3 通りの対立仮説がある。
ただし、1 回の検定で設定できる対立仮説は 1 個だけである。この後は帰無仮説を正しいと仮定して検定統計量を求め、その出現確率から帰無仮説を棄却するという流れになる。
2. 検定統計量を求める
検定統計量には、例えば以下のようなものがある。検定統計量の名前 (z 値、t 値など) がそのまま検定の名前 (z 検定, t 検定) として使われることが多いようである。
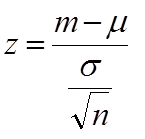
z 検定に用いる検定統計量、z 値。 |
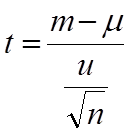
t 検定に用いる検定統計量、t 値。 |
3. 判断基準を定める
検定統計量は適当に定められたわけではなく、正規分布
normar distribution や t 分布
t distribution など
この確率は P 値 P value と呼ばれる。P 値が有意水準 level of significance と呼ばれる値よりも低いとき、一般に「帰無仮説が棄却された」ということになる。
これは、「帰無仮説では説明できないほど珍しいことが起きた」ということである。有意水準としては 5% (0.05) や 1% (0.01) がよく用いられる。この値を予め設定しておく。
4. 仮説を判定する
最後に、得られた検定統計量および有意水準を用いて、仮説を判定する。具体例の方がわかりやすいと思うので、z 検定 のページを参照して頂きたい。
広告
白鳥の例え: なぜわざわざ否定するための仮説を立てるのか?
集めてきたデータを使って、
例えば、「白鳥は白い」という仮説が正しいことを証明するのはどうすればいいだろうか? 仮に 100 羽の白鳥を集めてきて、それが全て白かったとしても、これは仮説の証明にはならない。今回のサンプルに、たまたま黒い白鳥が含まれていなかっただけかもしれない。
サンプルが 1000 羽になっても 10000 羽になっても同じである。この仮説を証明するには、世界中の全ての白鳥について調査を行わねばならず、これは標本調査ではないため、仮説検定とは無縁な研究になる。
一方、
そのために、仮説検定では帰無仮説を「否定する」ためのデータを集めてくることになる。
歴史
仮説検定の考え方は、1933 年にネイマンとピアソンによって提唱された (3)。
広告
References
- MATLAB による仮説検定の基礎. Web pdf.
佐藤弘樹、市川度 2013.
|
生存時間解析 について平易に書いた数少ない解説書。 統計のなかでも、生存時間解析はそれだけで 1 冊の本になるほど複雑なわりに、ANOVAや t 検定などと違い使用頻度が低いため、とっつきにくい検定である。 この本では、とくに |
|
- なるほど統計学園高等部. Link.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
