t 検定の原理 #1:
母分散が未知の場合の母平均の検定 (一標本 t 検定)
UB3/statistics/group_comparison/t_test_mean_principle
このページの最終更新日: 2025/11/23- 概要: t 検定とは
- 例題
- t 値の計算
- t 値の分布から確率を計算、有意差判定
広告
概要: t 検定とは
t 検定とは、t 分布に従う
- ある標本集団 (1 群) の母集団の平均値が特定の値に等しいかどうか
- 2 群の母集団の平均値が等しいかどうか
- 回帰直線を引いたときに、その勾配が 0 に等しいかどうか
このページでは、t 検定の原理を理解するために、もっともシンプルな t 検定である 1 番、つまり「母分散が未知の場合に、母平均がある値に等しいかどうか」という検定を行う。
やっていることは z 検定と非常によく似ており、仮説検定と z 検定のページを理解していることが前提である。より深く理解したい場合には、以下の順番に読むことを推奨する。
- 仮説検定
- z 検定
- t 検定の原理 #1: 母平均の検定: このページ
- t 検定の原理 #2: 対応のある t 検定
- t 検定の原理 #3: 正規分布、等分散の場合
- Welch の t 検定: 等分散を仮定できない場合
- Mann-Whitney の U 検定: 正規分布 を仮定できない場合。ノンパラ。
- 実践 1: Excel での t 検定
広告
例題
z 検定と同様に、文献 1 の例題を用いる。
|
例題 1 ある地域に立地する全てのスーパーマーケットの昨年の卵 1 パックの平均価格は、117 円でした。今年は、地域からランダムに 20 店舗を選び、卵 1 パックの値段を調査することになりました。結果は、次の通りです。 119; 117; 115; 116; 112; 121; 115; 122; 116; 118;109; 112; 119; 112; 117; 113; 114; 109; この結果から、地域内全てのスーパーマーケットの今年の卵 1 パックの平均価格は、117 円であるといえるでしょうか? なおデータは正規分布に従うが、 |
仮説検定のページの流れに従い、
帰無仮説: 平均価格は 117 円である。
対立仮説: 平均価格は 117 円ではない。
のように仮説を設定する。検定統計量 z を算出するには母集団の標準偏差 σ が必要であるが、今回は未知なので、
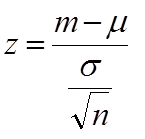
|
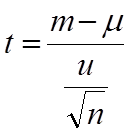
|
|
z 検定に用いる検定統計量、z 値。 |
t 検定に用いる検定統計量、t 値。 |
上の 20 個の値から計算すると、t = -2.1379 となる。そこで次に、この -2.1379 という値が現れる確率がどれだけ小さいかを検討することになる。
t 値の分布
z 値は標準正規分布に従う値であったが、
t 分布表 (2) を以下に載せておく。
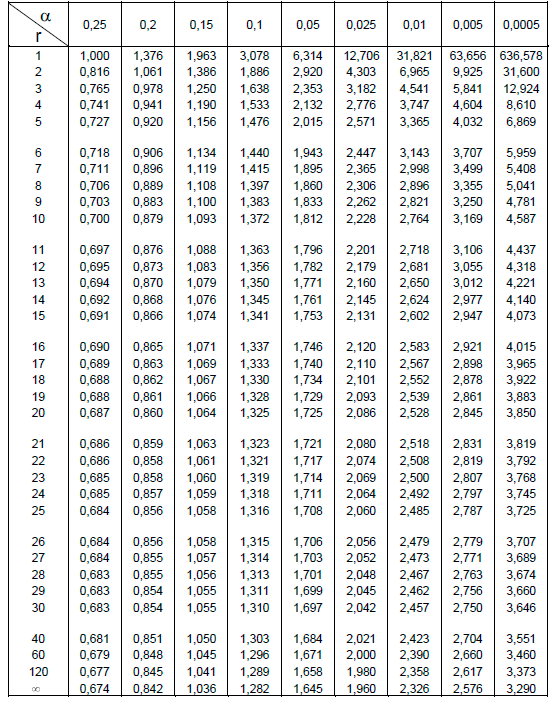
例題の場合、自由度は 19 になる。有意水準 5% での棄却域はプラスマイナス 1.729 になるため、帰無仮説は棄却される。つまり、この条件で - 2.1379 という t 値が現れる確率は 5% 以下と極めて低いことになる。したがって、「平均価格は 117 円とは有意にずれており、117 円であるとは言えない」という結論になる。
次はいよいよ、2 標本の平均値の差を検定する「普通の」 t 検定に移ります。「概要」のリンク から 対応のある t 検定のページへ進んで下さい。
広告
References
- MATLAB による仮説検定の基礎. Web pdf.
- "Tabla t" by Jsmura - Own work. Licensed under CC BY-SA 4.0 via Wikimedia Commons.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
