Welch の t 検定: 等分散を仮定しない t 検定

このページの最終更新日: 2024/09/30

概要: Welch の t 検定とは

このページでは、「データに対応がなく、かつ分散が等しいと仮定できない場合」に使われる Welch の t 検定を説明する。t 検定について原理からよく理解したい人は、以下の順にページを読んでもらいたい。

Welch の t 検定は、母分散が等しいと仮定できない場合の検定である。母分散は通常の場合未知であるので、2 つの標本集団の分散から推察するしかない。標本集団の分散が大きく異なっている場合は、母分散が等しいと仮定できないと推論することになるだろう。

この場合も、もちろん帰無仮説は等式で表されるので、

帰無仮説: 標本集団 A および B の平均値は同じである。
対立仮説: 標本集団 A および B の平均値は同じでない。

となる。これまでと違うのは、検定統計量の定義だけである。

左は、t 検定の原理 #3 で示した、等分散を仮定できるときの t 値である。どちらの t 値でも、Xa, Xb は標本集団 A および B の平均値、n_a, n_b は標本数。違うのは分散の部分である。

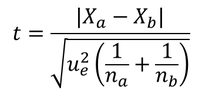
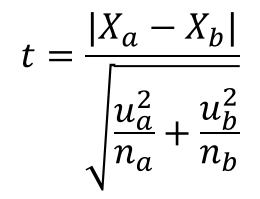
u_e² は併合分散で、これは分散が等しい場合にのみ使うことができる。

u_a²、u_b² は標本集団 A および B の標準不偏分散で、分散が等しいと仮定できないのでこれらを別々に用いなければならない。

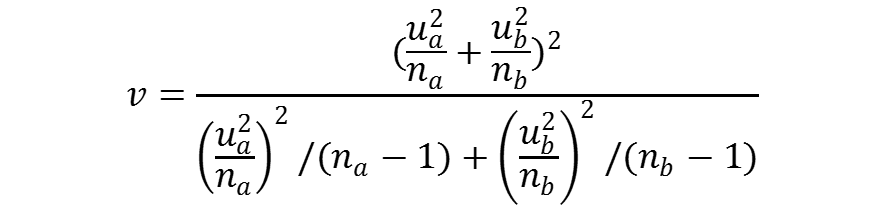
右側の Welch の t 検定の t 値は、残念なことに近似でしか t 分布に従わない。逆に言えば、この近似を編み出したことが Welch の功績なのだろう。さらに自由度 v も近似であり、以下の式で表される。整数になる場合はその値を、ならない場合はもっとも近い値を自由度として扱う。

このようにして算出した Welch の t 値は、近似ではあるが t 分布に従うことになる。したがって、以降の手順はこの t 値が出現する確率がどの程度小さいかを求めるということで、これは他の t 検定と同じである。

ここでは以降の手順の解説は省略する。「概要」の部分の目次から、ノンパラメトリックな検定へ進むこと。

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。