カイ二乗検定・適合度の検定: 原理と Excel による解析

UB3/statistics/group_comparison/chi_square

このページの最終更新日: 2024/09/30

内容が増えてきたので、以下の 2 項目はカイ二乗検定・独立性の検定のページに移動しました。

概要: カイ二乗検定とは

カイ二乗検定 chi square test とは、カイ二乗分布に従う統計検定量を用いる検定の総称である (1)。

の 2 つがよく用いられる。

このページでは、適合度の検定について原理と方法を説明する。統計・仮説検定の基礎知識を前提としているので、このあたりが不安な人は、以下のリンクも参照のこと。

適合度の検定 goodness-of-fit test は、標本集団の分布が母集団の分布と一致しているかどうかを判定する検定である。

血液型の例 (2) がわかりやすかったので、これを例示する。数字は元のページとは変えてある。

問題

日本人の血液型の分布を A 型 40%、B 型 20%、AB 型 10%、O 型 30% とする。以下の血液型のデータは、日本人全体の分布と同じとみなしてよいか？

A 型 35 人、B 型 18 人、AB 型 6 人、O 型 41 人

解答

以下のように、期待度数 (比率から期待される度数) と観測度数 (実際のデータ) を比較する。

カイ二乗値は、以下の式で与えられる。

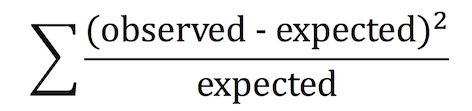
実際に数字をあてはめてみると、

(35 - 40)²/40 + (18 - 20)²/20 + (6 - 10)²/10 + (41 - 30)²/30 = 6.46

となる。この値がカイ二乗分布に従うことになる。なぜこの検定統計量がカイ二乗分布に従うのかは難しい問題なので、実際に検定を使いたいだけの場合は深く考えずに受け入れるのが良い。

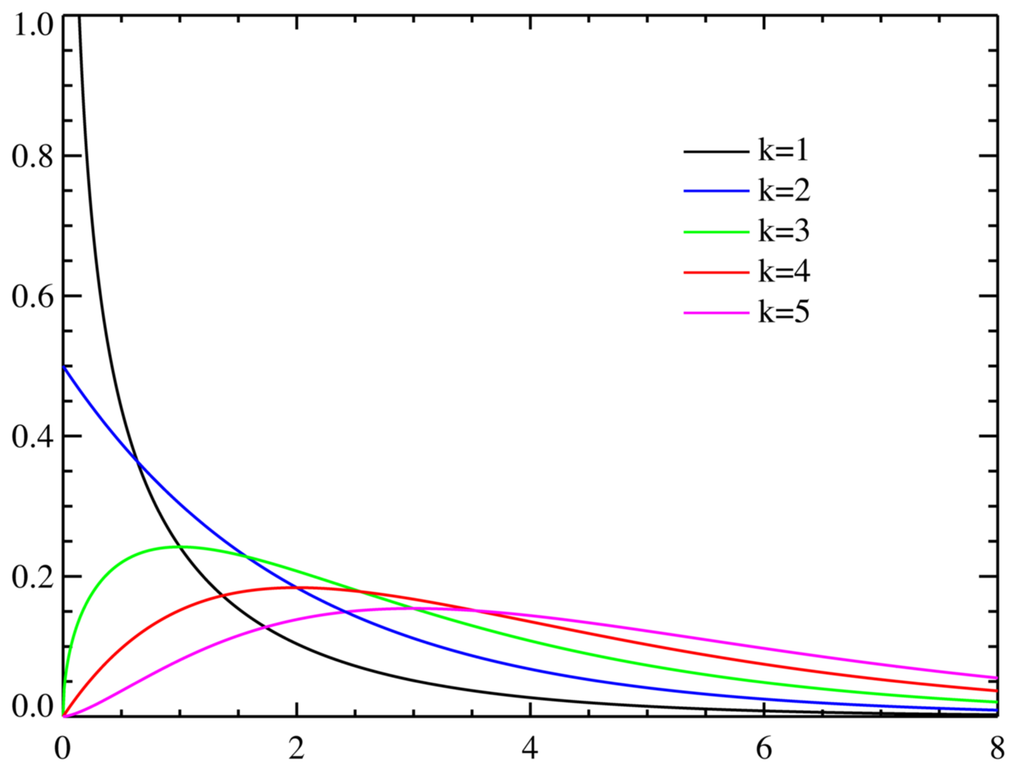
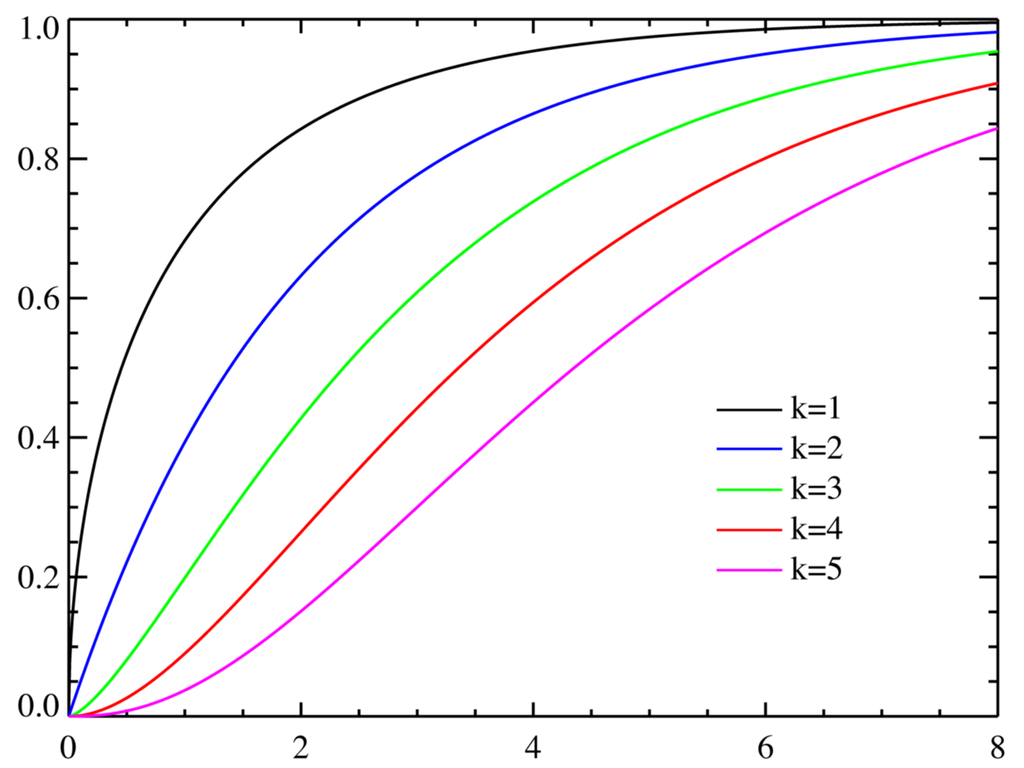
カイ二乗分布とは、以下のような分布である (Public domain)。左が確率密度関数、右が累積密度関数。正規分布や t 分布のような対照的な分布ではないので、右側確率、左側確率を論じるときには注意が必要である。

次に、自由度 degree of freedom を調べる。この場合、血液型が 4 タイプなので自由度は 3 である。もう少し詳しく言うと、自由度は次の式で計算される。

自由度 = (観測度数の列の数 -1) x (観測度数の行の数 -1)

観測度数のかわりに期待度数を使っても、全く同じである。ただし、この例のように列または行が 1 のときは、0 でなく 1 を使う。

自由度が 3、有意水準 0.05 のとき、下の表 (2) からカイ二乗値は 7.815。実際に得られた値はこれよりも小さいので、与えられた血液型データは日本人全体の分布と有意に異なるとは言えない、と結論できる。

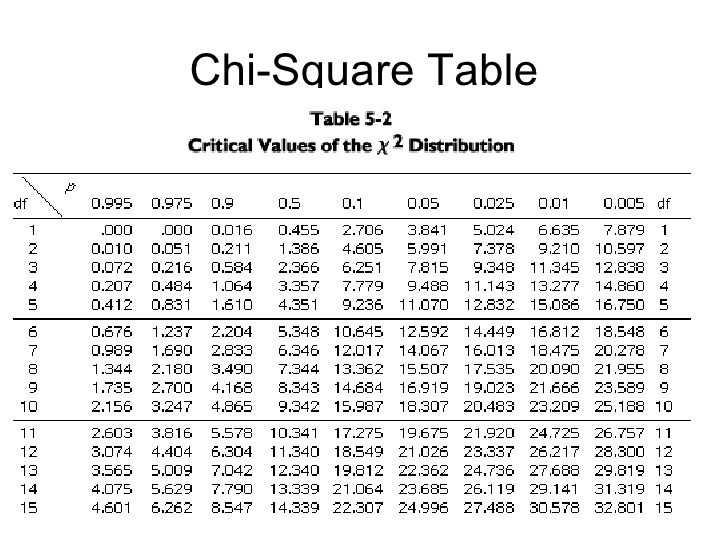
期待値からのずれが大きくなると、カイ二乗値も大きくなる。カイ二乗値が大きいと、「2 つの集団は有意に異なる」という結果が得られやすくなる。

以上の検定手順はわりと納得できるものだと思うが、最後のステップがとても原始的に見える。いまどき、本を見て P 値を推定するというのは流行らないだろう。

Excel には、カイ二乗値と自由度から P 値を算出する関数がある。種類がいくつかあるので、正しいものを使うようにしよう。以下は Office365、2020 年時点で Excel に備わっているカイ二乗検定の関数である。

chisq.dist	Chi-squared distribution で、カイ二乗分布の確率密度関数および累積密度関数を求める。chisq.dist(x, 自由度, 関数形式) で、x はカイ二乗値、自由度は自由度、関数形式は TRUE なら累積密度関数、FALSE なら確率密度関数である。上の例に従い、7.815 というカイ二乗値を使ってみる。chisq.dist(7.815, 3, TRUE) = 0.950006097 という値になるはずである。1 からこれを引くと、P 値の 0.05 が算出される。
chisq.dist.rt	カイ二乗分布の右側確率の値を返す (3)。chisq.dist(x, 自由度)。chisq.dist(7.815, 3) = 0.049993903 となる。
chisq.test	実際には、この関数を一番よく使うと思われる。独立性の検定によく使われる関数なので、独立性の検定のページで説明している。ページ上の目次リンクからどうぞ。
chisq.inv	chisq.inv(x, 自由度) で、カイ二乗分布の左側確率の逆数を返す。ちょっとどう使うのかよくわからない。

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。