1. カイ二乗検定: 独立性の検定 by Excel
   1. 期待度数の表を作る
   2. カイ二乗値を計算する
   3. chisq.test 関数で p 値を計算する
2. カイ二乗検定の実際
   • カイ二乗検定の Cochran’s rule
3. 生存率をカイ二乗検定で比較することの是非

カイ二乗検定: 独立性の検定 by Excel

このページでは、与えられた 2 つの集団の分布が一致しているかを判定する 独立性の検定 について解説する。カイ二乗検定・適合度の検定 のページの続きなので、まずはリンク先のページを読むことをお勧めする。

適合度の検定 goodness-of-fit testでは、母集団の分布をそのまま期待値とした。しかし、独立性の検定では母集団が与えられていないため、2 群のデータから期待値を算出する必要がある。違いはそれだけである。同じように、問題を解きながら実際に作業するのがいいだろう。

問題 治療法 A, B を比較した結果、治療によって回復した人、回復しなかった人の割合として以下のようなデータが得られた。2 つの治療法の効果は有意に異なっていると言えるか？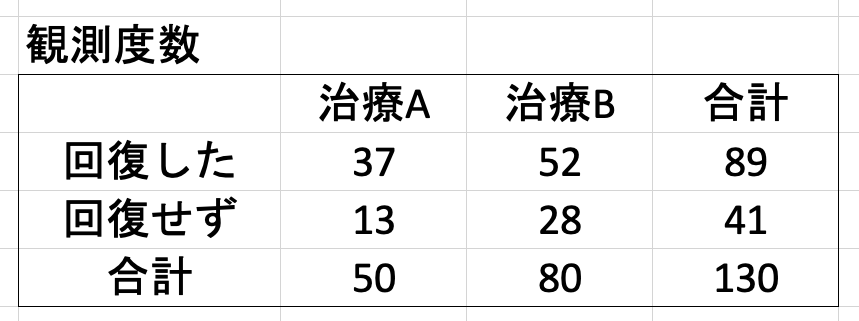

解答

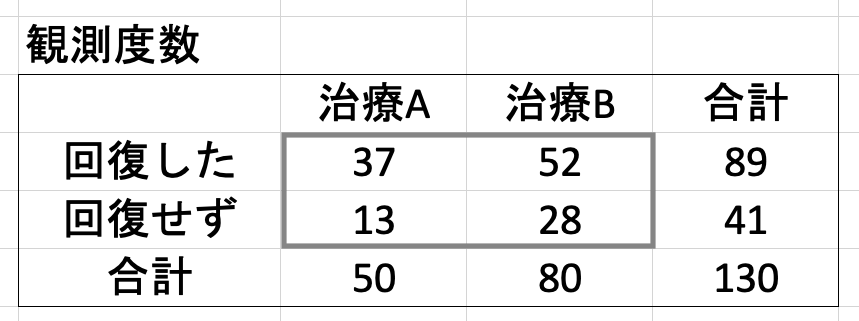
1. 期待度数の表を作る

以下のように、期待度数は、合計値から算出する。この場合、「治療 A と治療 B で頻度に差がない」というのが帰無仮説になる。

偏りがない場合、「回復した」と「回復せず」の割合は、治療 A でも治療 B でも 89 : 41 になるはずである。よって、「治療 A」「回復した」の期待値は、50 * 89 / 130 = 34.2308 となる (黄色のハイライト)。

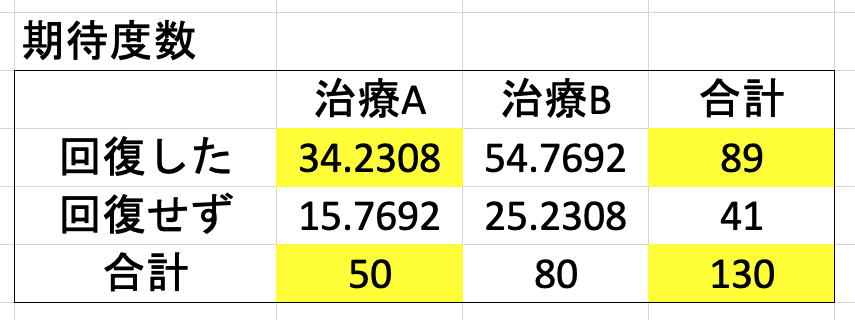
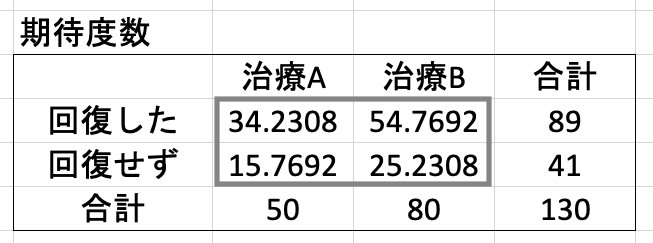
これと同様にして、4 つの期待度数を計算する。

• 54.7692 = 80 * 89 / 130
• 15.7692 = 50 * 41 / 130
• 25.2308 = 80 * 41 / 130

要するに、その行・その列の合計値を掛け合わせて、総計の 130 で割っているだけ。これで観測度数と期待度数が得られたので、カイ二乗値を計算することが可能になる。

2. カイ二乗値を計算する

カイ二乗値は、以下の式で与えられる。

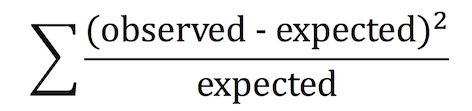
実際に数字をあてはめてみると以下のようになり、これがカイ二乗分布に従うわけである。あとは chisq.dist.rt 関数でカイ二乗値 1.15429 と自由度 1 から計算してもいいし、chisq.test 関数を使ってもいい。

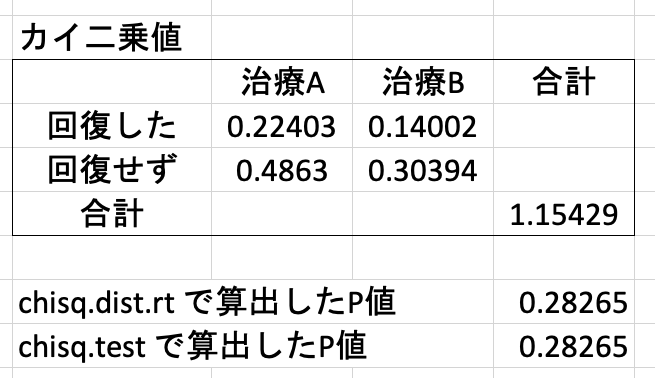
3. chisq.test 関数で p 値を計算する

chisq.test 関数を使うなら、自分でカイ二乗値を計算する必要はない。chisq.test(実測度数の範囲, 期待度数の範囲) とすればよい。具体的にはこんな感じに、4 つのセルを選択する。

当然のことながら、P 値はいずれの方法でも同じになる。この場合、P = 0.28265 なので、治療法 A と B は有意に異なるとは言えない、という結論になる。

カイ二乗検定の実際

実際にカイ二乗検定をする際の注意点もメモしておく。

• パーセンテージを直接使った検定はできない。2 つの値、X% と Y% があるとすると、これらを算出したもとの数 A, B, C および D があるはずである (X% = A/B * 100、Y% = C/D * 100)。この整数値 A から D を用いて検定を行う。

カイ二乗検定の Cochran’s rule

カイ二乗検定は近似を使っているので、期待数が大きくなるほど正確になる。期待数が 5 未満のマス目が全体の 20% 以上のときには、カイ二乗検定を用いてはならない というルールがあるようだ (1, もとの文献は 2)。

私は 2 x 2 以外のカイ二乗検定をあまり見たことがないのだが、この書き方によるとマスはもっと増やせるようだ。2 x 2 の場合はマス 1 個でも 25% なので、つまり期待度数が 5 未満のマスがあるとダメということになる。

生存率をカイ二乗検定で比較することの是非

同じデータで「回復した」「回復せず」を「生存」「死亡」に置き換えると、2 群の生存率の違いをカイ二乗検定で比較できるように思える。しかし、これは完全な間違いとは言えないかもしれないが、ベストの方法ではない。

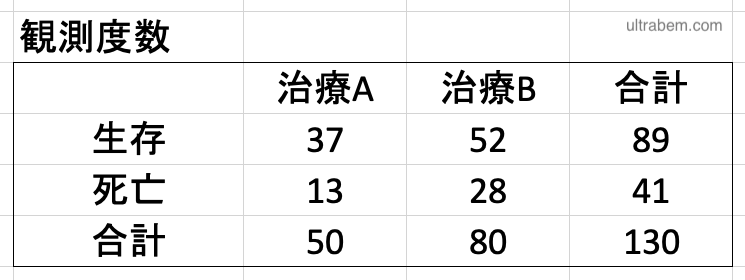
理由は以下の通りで、Log-rank 検定 を使うべきとしている (3)。

• 打ち切り censored observation を考慮に入れていない。
• 2 つの群の follow up time の違いを考慮に入れていない。つまり、ある治療から 5 年以内の効果と、他の治療から 10 年以内の効果を比較してしまう可能性がある。

2 番目は少し解釈が難しかったが、おそらくこういうことだと思う。カイ二乗検定の場合、使えるデータのタイムポイントは 1 点のみであり、もっている情報の一部しか利用していない。

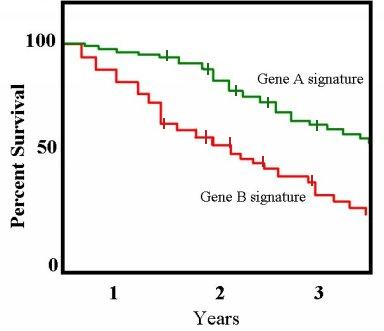
例えば以下のような生存率のグラフがあるとき、3 年の観察期間終了後のデータで統計検定を行う場合、カイ二乗検定 では 1 年目の死亡と 3 年目の死亡を同じものとして考えてしまう。一方、log-rank 検定の考え方はカイ二乗検定に近いものの、生存期間の全体にわたって比較する ようになっている。

このことから、log-rank の方が適した検定と言える。

References

1. χ2乗検定とFisher正確確率検定 ～χ2乗検定の不適切使用をしていませんか？～ Link: Last access 2021/06/30.
2. Cochran, 1954a. Some methods for strengthening the common x2 tests. Biometrics 10, 417-451.
3. Brazauskas, 2015a. Incorrect use of chi-square test for analyzing time-to-event data. Medical College of Wisconsin, Devision of Biostatistics newsletter 21.
4. 2 つの生存率の比較. Link: Last access 2021/06/30.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。