ピアソンの相関分析・相関係数: 計算方法など
UB3/statistics/correlation/pearson
このページの最終更新日: 2025/11/23- 概要: ピアソンの相関とは
- Excel を使った相関分析
- ピアソン相関係数の算出方法
- P 値の算出方法
- 相関係数 ρ は足し算できない
- R を使った相関分析 → R cor.test へ
- MATLAB を使った相関分析 → MATLAB corr 関数 へ
広告
概要: ピアソンの相関とは
ピアソンの相関は、2 つの変数 x と y が正規分布 normal distribution しているとみなせるとき、それらの間にどの程度の相関があるかを調べる方法である。正規分布を仮定しているので、パラメトリックな統計手法である。
ピアソンの相関では、2 組の数値からなるデータ列 (xi,yi) ただし (i=1,2, ... n) があるとき、相関係数が以下の式で与えられる。通常は
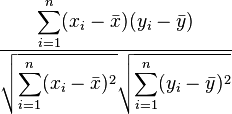
相関係数は、正の相関のときには正の値を、負の相関のときには負の値をとる。
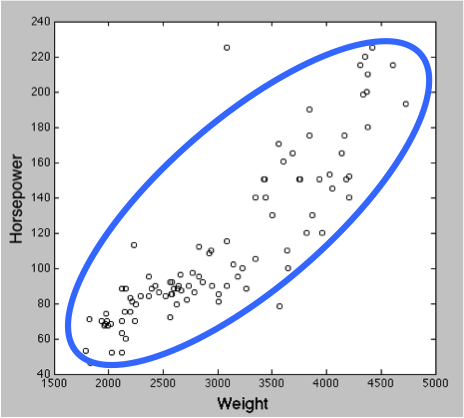
車の重量と馬力の正の相関。ρ = 0.8471。
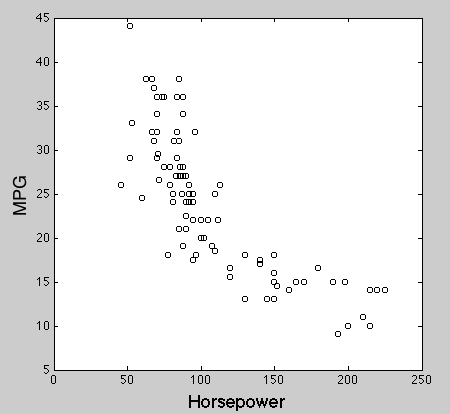
車の重量と燃費の負の相関。ρ = -0.7440。
このページには、Excel を使ったピアソン相関係数の算出方法と、その相関が
広告
Excel を使った相関分析
私は、相関分析には基本的に R の cor.test 関数を使っている。ピアソン、スピアマン、ケンダールのいずれにも使える便利な関数であり、ページ上方の「R cor.test へ」という部分にリンクがある。
このページでは、あえて Excel を使った方法をまとめておく。理由は、
ピアソン相関係数の算出方法
cor.test と同様に、R 組み込みデータセット swiss を使ってみる。swiss はスイスの各地方における出生率と、さまざまな社会要因のデータである。最も関係していそうな Examination と Education に相関があるかどうかを調べてみよう。
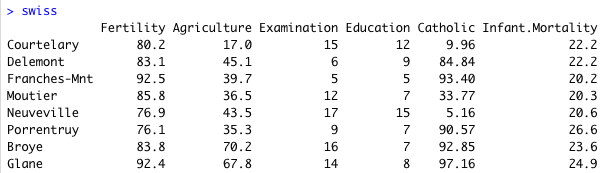
まずは、Education と Examination を Excel にコピーして、散布図を書いてみる。もちろん R の場合と同じように、正の相関がみられる。
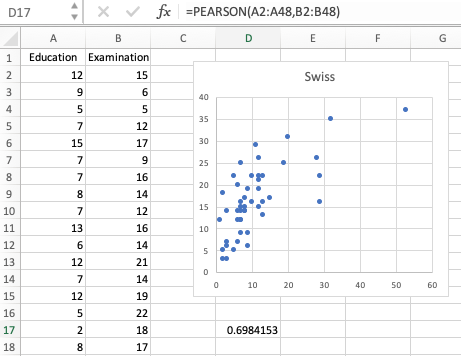
Excel には、ピアソンの相関係数を算出する関数があるので、ここまでは簡単である。すなわち、PEARSON という関数を使って = PEARSON(範囲1, 範囲2) とする。
図では、0.6984153 がピアソンの相関係数である。
P 値の算出方法
Excel では相関係数の算出はできるが、PEARSON 関数では P 値が計算されない。実際に論文を 査読 していても、相関係数だけを示して P 値が示されていない例がかなりあるので、Excel のこの仕様が関係しているのではないかと思っている。
この検定の 帰無仮説 は、「相関係数が 0 に等しい」である。つまり、
文献 1 の方法で、Excel で P 値を算出する方法を紹介する。以下のような手順になる。
- まず PEARSON 関数で相関係数 ρ を算出する。
- 相関係数と 自由度 から、t 分布に従う検定統計量を算出する。
- TDIST 関数で、その t 値が得られる確率、すなわち P 値を算出する。
2 番の検定統計量は、相関係数 ρ を用いて以下の式で算出できる。
Excel では、1/2 乗すなわち平方根は SQRT 関数で計算できるので、実際に入力するのは以下のようになる。
なお、サンプル数は片方の群であり、そこから 2 を引いたものが自由度になる。この例では Education, Examination にそれぞれ 47 個のデータがあるので、自由度は 47 - 2 = 45 である。
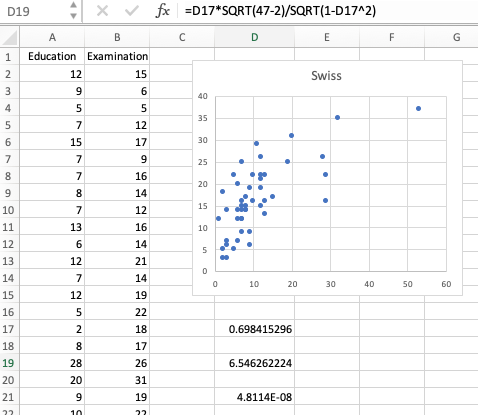
このように計算すると、t 値が 6.546262224、P 値が 4.8114E-08 と計算される。有意水準を 0.05 とすると、P 値がそれよりも小さいので、この相関は有意である。
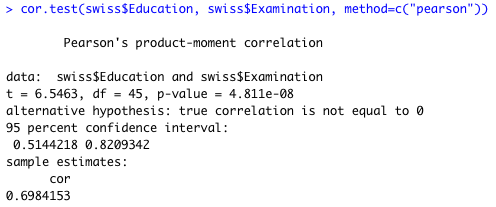
同じデータを使って R で解析しても、t 値および P 値は同じになることを確認しておこう。
相関係数 ρ は足し算できない
ピアソンの相関係数は additive でないので、足し算をすることはできない。よって、単純に 相加平均 をとることもできない (2)。
理由として、
平均を求めたい場合は、まず各係数を Fisher の Z を使って変換し、Z 値として相加平均をとったあと、相関係数に戻す必要がある。この際、相関係数を計算した 2 セットのが両方とも正規分布していないと、エラーが大きくなる (3)。つまり、ピアソンの相関係数ならこのようにして平均をもとめることができるが、ノンパラメトリックなスピアマンの相関係数の平均は、この方法では求められないということになる。そもそも、ノンパラメトリックな場合は平均値にあまり意味がないので、計算する必要性も低い。
広告
References
- Deus ex machinaな日々. エクセルで相関係数のp値を出す. Link: Last access 2020/07/15.
- 標本数による限界値. Link: Last access 2020/07/15. 標本数によって、相関係数が有意になりうるかどうかが決まっており、その一覧表が載っている。
- Average of Pearson correlation coefficient values? Link: Last access 2020/09/03.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
