確率変数と確率分布: 定義、実例など
UB3/statistics/basics/random_variable
このページの最終更新日: 2025/11/23- 確率変数とは
- 確率変数の離散型と連続型
- 確率分布とは
- 離散型の確率分布
- 離散型分布の例
- 連続型の確率分布
- 連続型分布の例
- 累積分布関数
広告
概要: 確率変数とは
確率変数 random variable とは、それぞれの要素が確率 probability をもつ変数 variable のことである。なお変数 variavble とは、未知の数、不定の数を示す文字記号のことで、教科書ではよく x, y, z などで表される。
言い換えると、
- サイコロの目を x とおいてみる。x は 1 から 6 までの整数値をとる変数である。これ対して、サイコロを振るという行為を考えた場合、x のそれぞれの値は 1/6 という確率を有することになる。したがって、サイコロの目は確率変数である。
- ある人の体重 BW を測定したときに、ある一定の確率で BW = 60 kg という値が出るだろう。したがって、体重は確率変数である。
身長、血糖値、寿命など、通常の実験で測定されるような値は、基本的には確率変数であると考えて良い。

確率変数の離散型と連続型
確率変数は、大きく以下の 2 種類に分けることができる。
離散型の確率変数 discrete random variables連続型の確率変数 continuous random variables
離散型とは、サイコロの目のように 1, 2, 3... といった決まった値を取り、その中間値がないものである。
連続型とは、身長、体重のように連続した値を取りうるもので、無限の値が存在する。
広告
確率分布とは
確率分布 probability distribution とは、
離散型の確率変数と、連続型の確率変数では、確率分布の定義も異なっている。
- 離散型: 一般に可算集合 {x1, x2, ...} の中の値をとる確率変数 X は離散型といわれ、それぞれの値の確率 P(X=xk) = f(xk) を確率分布という (3)。
- 連続型: 確率変数 X のとる値 x が実軸上の領域 A に含まれる確率を A の関数として表したもの。確率空間 (Ω, B, P) の測度、すなわち確率 P によって P(X ∈ A) のように与えられる (2)。
確率分布は、数式で表すことができる。最も単純な例として、「6 の目しか出ないサイコロを振ったときに出る目 X」という変数を考えてみよう。この場合、x = 6 となる確率は 100% である。
よって、「6 の目が出る確率」を P(X=6) と表すと、P(X=6) = 1 がこの変数を表す数式である。このような、確率分布を記述する関数を
離散型の確率分布
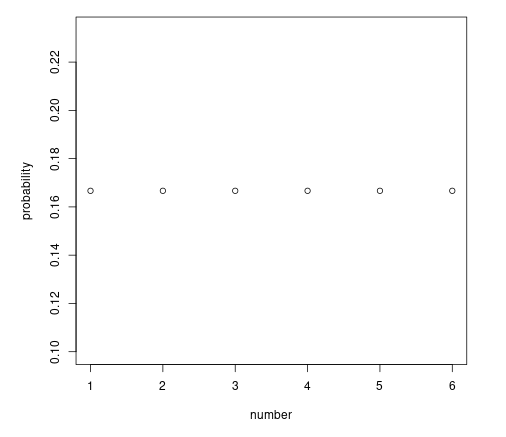
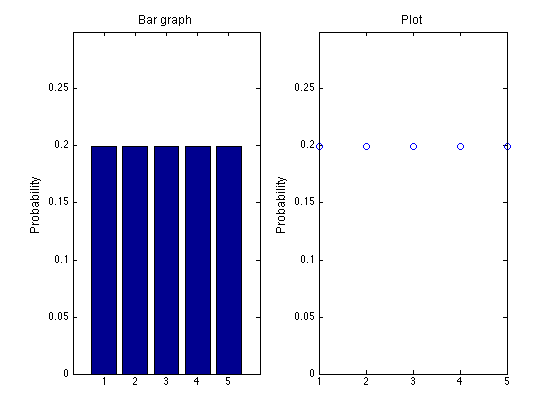
もう少し複雑な実例として、正 5 面体の理想的なサイコロを考えてみる。確率変数は 1, 2, 3, 4, および 5 であり、それぞれの値がもっている確率は 0.2 である (割り切れるように 6 面体でなく 5 面体のサイコロにした)。
視覚化するならば図のようになる。
この例では、サイコロは 1 - 5 以外の値をとらないため、離散型の確率分布 discrete probability distribution と呼ばれる。
この場合の確率密度関数は、
P(X=1) = P(X=2) = P(X=3) = P(X=4) = P(X=5) = 0.2
となる。次に述べる連続型の確率分布では、もう少し関数らしく見える確率密度関数が得られる。
このグラフは MATLAB で作ったが、R で作った六面体サイコロの確率密度関数も示しておく。
離散型分布の例
| データ範囲 | 分布の名前 | 説明 |
二項分布 |
コインの表か裏か、成功か失敗かなど、2 種類の結果しか得られない試行を このような試行を n 回行ったとき、A が何回起こるか (または B が何回起こるか) を示す確率分布が二項分布である。 |
|
有限 |
ベルヌーイ分布 |
ベルヌーイ分布は、二項分布で n = 1 のときの分布である。 |
有限 |
一様離散分布 |
上のサイコロの例のように、有限な数の事象があり、かつそれぞれの確率が等しい分布。「同様に確からしい」という表現がよく使われる。 |
無限 |
ポアソン分布 |
1 時間当たりに受け取るメールの数、年間の交通事故数のように、自然数を要素とする確率変数 X が従う分布。 |
負の二項分布 |
連続型の確率分布
身長や体重は、サイコロの目のように離散的な値をとらず、連続的な分布を示す。この場合は、上記の例のように 0.2 などの数値の羅列で分布のパターンを記述することはできないため、関数で記述する必要がある。
連続型の確率変数の場合も、分布のパターンを確率分布といい、それを記述する関数を確率密度関数という。
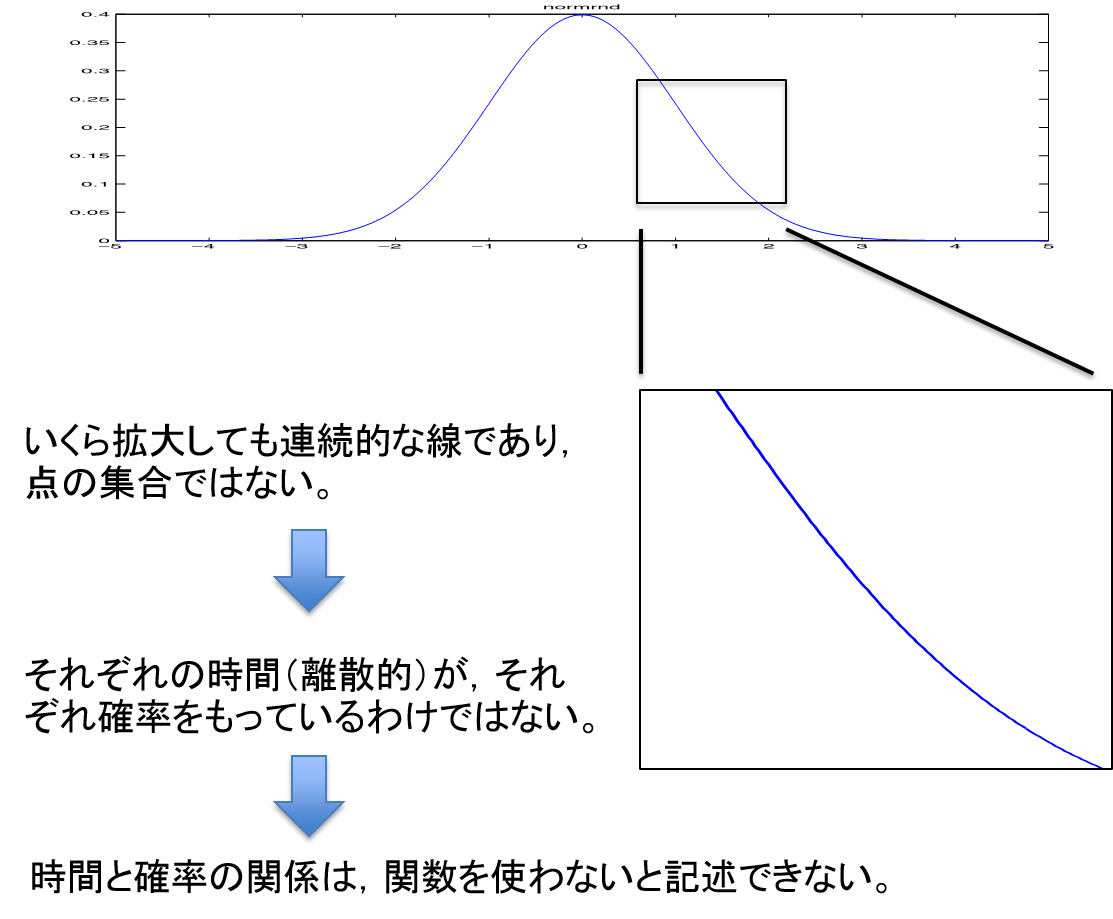
たとえば、太郎が学校を出てから家にたどり着くまでの時間を表すと、おそらく以下のような正規分布になるだろう。ここで重要なのは以下の点である。
- 時間は、はサイコロの目のように有限な数の要素にわけることができない。
- つまり、グラフの線はいくら拡大しても線であり、点の集合ではない。
- 逆に言えば、たとえば太郎が正確に 30 分で家にたどり着く確率はゼロである。
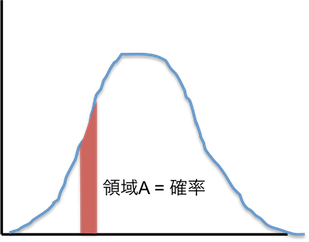
太郎が正確に 30 分で家にたどり着く確率はゼロであるが、「30 - 35 分」のように範囲を与えることで、積分によって確率を指定することができるようになる。
連続型分布の例
| データ範囲 | 分布の名前 | 説明 |
|---|---|---|
| 有限 | ベータ分布 |
分布形状の自由度が高く、様々な分布にフィットさせることができる。 |
| 有限 | ジョンソン SB |
ベータ分布と同様に自由度が高い。平均、標準偏差、歪度、尖度を自由に調整できる。樹木の幹の直径の分布? |
| データ範囲 | 分布の名前 | 説明 |
|---|---|---|
半無限 |
指数分布 |
たまに起きる事象の「間隔」の分布。この分布に従って事故が発生すると、その頻度はポアソン分布になる。 |
半無限 |
対数正規分布 |
正規分布の対数。年収などがこの分布に従うらしい。 |
半無限 |
カイ二乗分布 |
カイ二乗検定 chi-square test に利用される。 |
半無限 |
F 分布 |
F 検定に利用される。 |
| データ範囲 | 分布の名前 | 説明 |
|---|---|---|
無限 |
||
無限 |
コーシー分布 |
正規分布に似るが、外れ値の多い分布である。 |
無限 |
ロジスティック分布 |
正規分布に似るが、裾が少し厚い。正規分布よりも式が簡単で扱いやすい。また、この分布の累積分布関数はロジスティック曲線であり、様々な分野で応用されている。 |
無限 |
t 分布 |
t 検定 に利用される。 |
無限 |
ワイブル分布 |
Weibull distribution は、物体の強度を統計的に記述するために Weibull によって提案された分布である。時間 t に対する故障率を、ワイブル係数 m の値として表すことができ、さまざまな分野に応用されている。 |
広告
累積分布関数
まず、確率変数 X が A 以下の値をとる事象を {X ≤ A} とする。決まった範囲でなく 「A 以下の全ての値」
-∞ ≤ X ≤ A であることに注意しよう。
このとき、この確率は P(X≤A) = F(x) という関数で表される。関数 F(x) を 累積分布関数 cumulative distribution function, CDF という。
横軸に x 、縦軸に F(x) をとり、累積分布関数の図を描いてみよう。以下のことから、大体の形をイメージできるだろう。
- F(x) はあくまで確率なので、正の値をとり、かつ 1 を超えない。
- x が ∞ のとき、F(x) は 「確率変数 Y が無限大以下である確率」 である。つまり F(x) = 1 である。
- 逆に、x が - 無限大に近づくと、F(x) は 0 に近づいてゆくだろう。
したがって、F(x) は F(x)=1 と F(x)=0 を漸近線とするグラフになる。
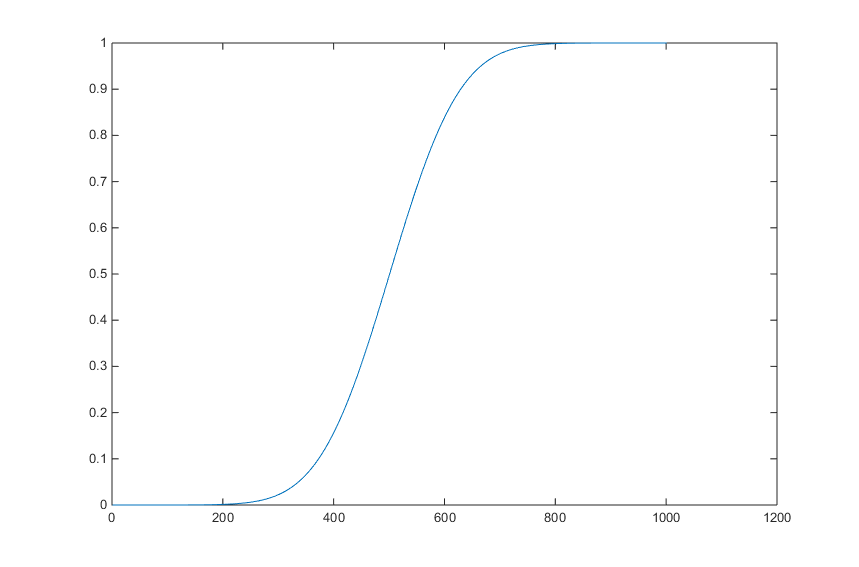
よく言われるのが、「
- 積分とは、関数と軸の間の面積を計算することである。
- 累積分布関数を微分すると確率密度関数になるのだから、逆に確率密度関数を積分すると累積分布関数になる。
これらのことを踏まえた上で、図 1 または図 2 で関数と X 軸の間の面積を左の方から(-∞ から)足し合わせていくイメージで考えてみよう。
- x は -∞ まで及んでいるが、x が小さいときは確率もとても小さいので、x を増やして行っても面積の増加はわずかである。
- x が 0 に近づくと、次第に増加率も大きくなっていく。
- この図は x = 0 に対して左右対称であり、かつ x = ∞ までの面積を全部足すと 1 になる。したがって、x = 0 のとき、ちょうど面積は 0.5 になり、そこから増加率が徐々に減ってゆく。
- x が正の ∞ に近づくと、増加率は非常に小さくなる。
References
- 確率と確率変数. Web pdf.
- Amazon link: 岩波 理化学辞典 第5版
: 使っているのは 4 版ですが 5 版を紹介しています。
- 統計学入門 (基礎統計学 I)
|
確率の基礎、確率分布、仮説検定、回帰などについてわかりやすく解説してある本である。 古い本であるが、レベルを落とさずに、わかりやすくかつバランスよく必要な内容を網羅しており、 付表として正規分布表、t 分布表、F 分布表がついており、これも意外と役に立つ。練習問題とその解答もついている。 |
|
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。