正規分布: 平均値と標準偏差で規定される釣鐘型の分布
UB3/statistics/distribution/normal_distribution
このページの最終更新日: 2025/11/23- 概要: 正規分布とは
- 正規分布の特徴
- 標準正規分布
- R で正規分布を作成し、ヒストグラムで可視化する
- 正規性の検定
- qq プロット
- Shapio-Wilk 検定
確率変数と確率分布 のページに、正規分布を含む分布の一覧があります。
広告
概要: 正規分布とは
正規分布 normal distribution とは、以下の確率密度関数 probability density function (PDF) で表される確率分布である。
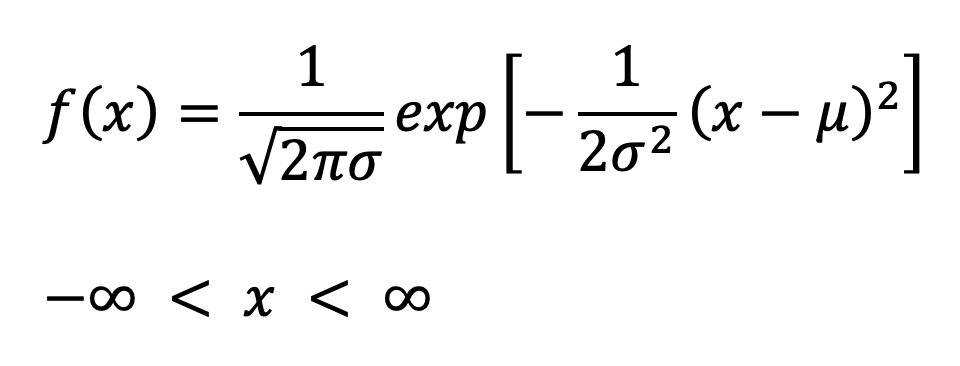
式は複雑に見えるが、ここでのポイントは、
平均値と分散を動かしてみて、グラフのパターンがどうなるかを調べた図が以下 (Public domain) である。平均値と分散によってグラフが変わること、どのグラフも同じような釣鐘型 bell-shaped の曲線であることがわかるだろう。
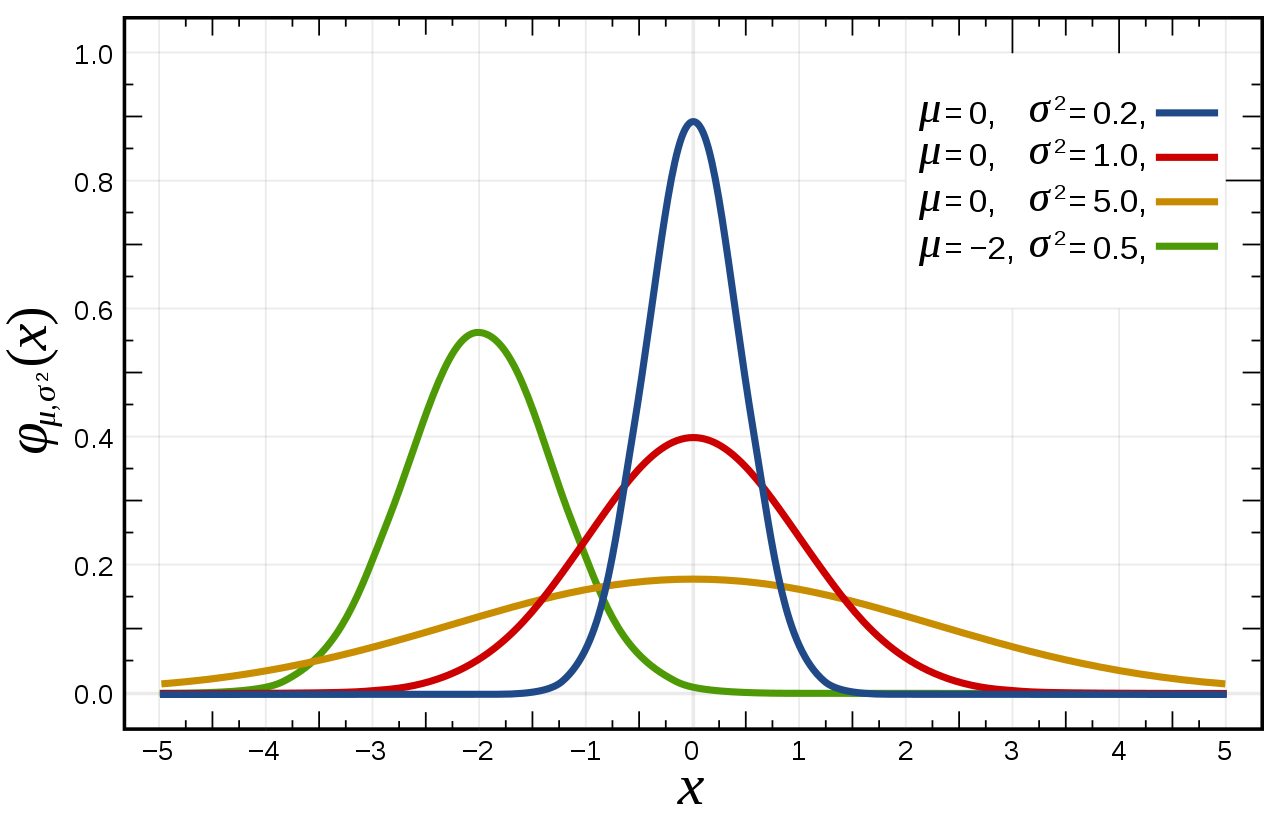
正規分布の特徴
このページ に便利そうな正規分布の図がたくさんあるが、以下の図 (Public domain) が一番情報量が多くて良さそうだったので、このサイトではこれを基本的に使うことにしたい。
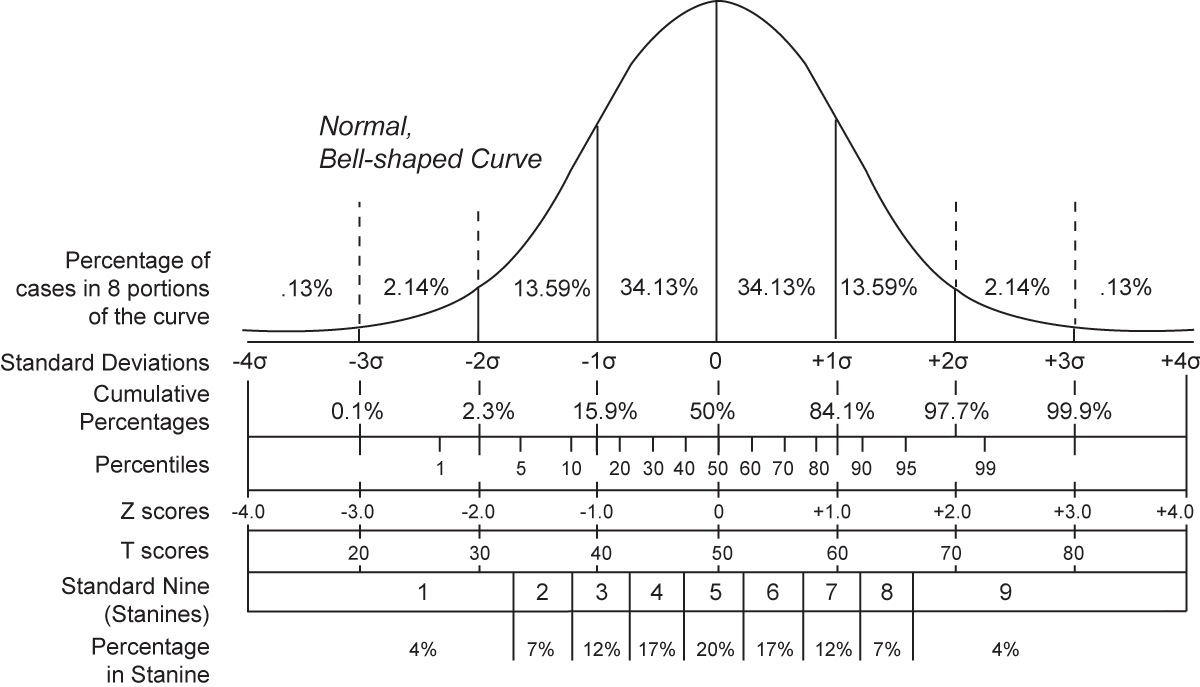
正規分布には、以下のような重要な特徴がある。
- 釣鐘型 bell-shaped の曲線を示す分布である。
- 平均値 mean、中央値 median、最頻値 mode が全て等しい。平均値はしばしば μ で表される。
- 標準偏差を σ としたとき、データの約 68% が μ ± σ の範囲に分布する (0 から ± 34.13% の範囲)。
- 同様に、約 95% が平均から 2 標準偏差の範囲内に収まる。
標準正規分布
平均値 0、標準偏差 1 の正規分布を、とくに標準正規分布 standard normal distribution という。
男性、女性の身長はそれぞれ正規分布に従うが、それを合わせると上の平らな分布になるらしい (1)。
R で正規分布を作成し、ヒストグラムにする
統計ソフト R には、rnorm という正規分布を作成するための関数がある。正規分布は平均値 μ および標準偏差 σ で指定される関数であり、実際のデータとしてはサンプル数 n も要素になる。よって rnorm ではこの 3 つを指定する。ただし、ギリシャ文字ではなく m と sd を使う。
n を 10 と 1000 にして、同じ平均と分散をもつ 2 つの正規分布、testnorm1 と testnorm2 を作ってみる。
testnorm1 <- rnorm(n=10, m=0, sd=1)
testnorm2 <- rnorm(n=1000, m=0, sd=1)
これを hist 関数でプロットしてみると、次のようになる。
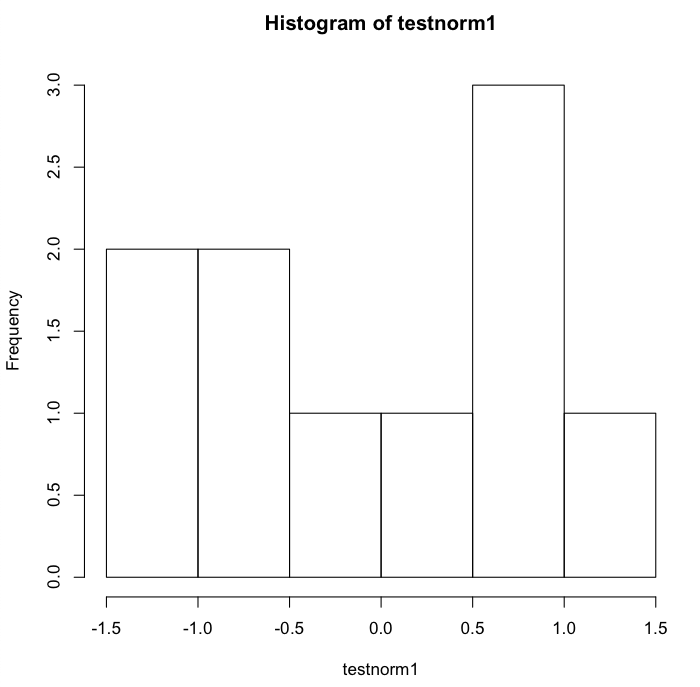
|
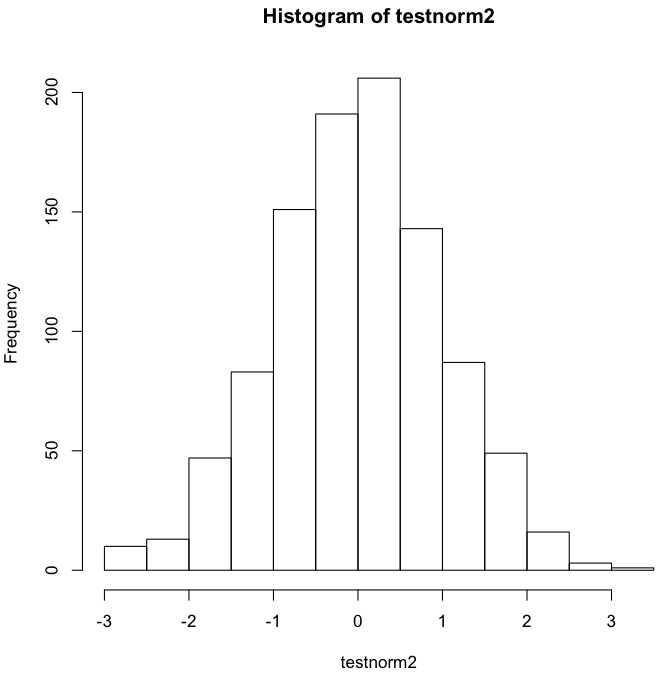
|
サンプル数が少ないと、正規分布していても全く釣鐘型に見えないが、サンプル数が増えるほど完全な釣鐘型に近くなる。
男性、女性の身長はそれぞれ正規分布に従うが、それを合わせると上の平らな分布になるらしい (1)。
正規性の検定
qq プロット
qq プロットは検定ではないが、あるデータセットが正規分布しているかどうかのデータを可視化するプロットであり、覚えておくと便利。R を使った方法を説明する。
R のベクトルデータ testnorm3 を作り、これを qqprot してみよう。
testnorm3 <- rnorm(n=1000, m=0, sd=1)
qqnorm(testnorm3)
qqline(testnorm3)
関数名は qqplot でないので注意。まず分布をプロットする qqnorm を実行。次の qqline は、このプロットに線を追加する。
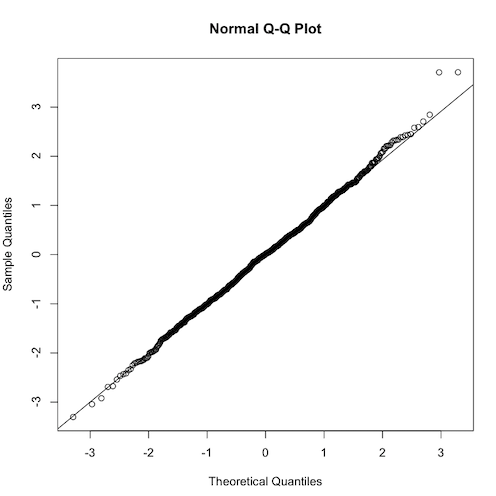
このプロットでは、X 軸および Y 軸はそれぞれ観測値の分位数 sample quantiles と理論的分位数 theoretical quantiles を示す。この 2 つの "quantile" が、qqplot という名前の由来である。qqline とは、両者が等しくなるような 45 度の線のこと。
Shapiro-Wilk 検定
データが正規分布しているかどうかの検定には、Shapiro-Wilk 検定がよく使われる。
統計ソフト R を使った検定方法を R の Shapiro-Wilk test のページにまとめたので、リンク先を参照のこと。
広告
References
- Distribution of adult heights. Link: Last access 2020/06/30.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
