R: glm 関数によるロジスティック回帰分析
UB3/informatics/r/regression_glm_logistic
このページの最終更新日: 2025/11/23広告
R による回帰分析
R では、回帰に以下のような基本関数が用意されている。このページでは、glm 関数を用いたロジスティック回帰についてまとめる。ロジスティック回帰とは、2 値データを目的変数とした回帰分析のことをいう。
lsfit |
最小二乗法による回帰 |
lm |
線形モデルによる回帰。lm 関数を用いた単回帰分析、lm 関数を用いた重回帰分析 のページも参照のこと。 |
glm |
一般線形モデルによる回帰。母集団の正規性を仮定できなくても使うことができる。ロジスティック回帰では、もちろん母集団は正規分布しないので、この関数を使うことになる。 |
nls |
Nonlinear least squares の略。関数を定義して非線形の回帰を行う場合に使う (参考ページ)。最小二乗法を使っている。 |
広告
「あとがき」で当サイトを参考にしたと書いてくれているラノベです。Kindle Unlimited で読めました。ストーリーと文章が良く、面白かったです。
glm() 関数の基礎
基本的な使い方は lm() 関数と同じである。
- glm の結果をオブジェクトとして保存する。複数の x がある場合、glm の基本形は lm(y ~ x1 + x2) である。+ を使っていくらでも x を増やせる。
- そのオブジェクトの詳細を summary 関数で表示する。
summary(result)
大きな違いの一つは family で関数を指定する点である。ロジスティック分析の場合は、binomial を指定する。binomial(link = "logit") のようにして、リンクする関数を指定できる。このページ に詳しい説明あり。binomial のデフォルトは logit なので、family = binomial と family = binomial(link = "logit") は同じ結果になる。
family では、以下のような関数を指定できる。
binomial |
ロジスティック回帰ではこれ。意味を検索すると「二項式」と出てくる。2 つのものから成り立っているという意味で、目的変数が 0 または 1 の値しかとらないことを意味している (参考: 二項分布)。 link は以下の関数を指定できる。
|
poisson |
ポアソン分布。離散値のときに使う。 |
gaussian |
実例 1: mtcars を使った分析
単変量のロジスティック回帰分析
R の 組み込みデータセット mtcars には、vs と am という二値変数がある。これを目的変数としてロジスティック回帰を実行してみる。
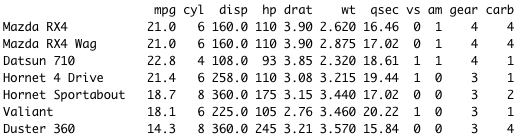
- 排気量 displacement、マイレージ/ガロン (燃費) mpg の数値が大きい。
- cyl と gear はシリンダーとギアの数で、整数値をもつ離散変数。
- vs と am は、エンジン (0 = V-shaped, 1 = straight) と Transmission (0 = automatic, 1 = manual) で、0 または 1 の二値変数である。
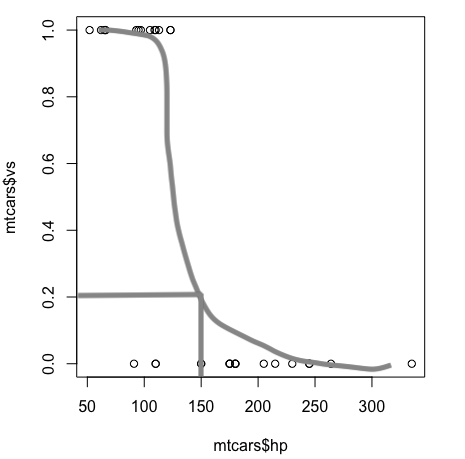
まずは単変量ということで、説明変数を hp、目的変数を vs とする。このような解析のときは、最初に散布図などを作ってデータを外観するのが基本である (参考: plot()関数による散布図の作成)。
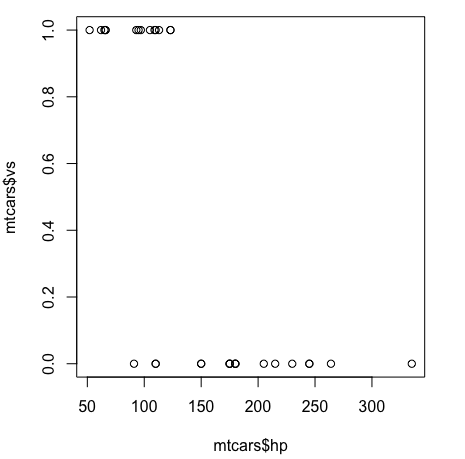
なんとなく、hp が低いと vs は 1 という関係がありそうである。馬力が低いエンジンはストレート型ということ。
これを無理に線形回帰すると、たぶんこんな感じになる (この線はマニュアルで適当に引いたもの。参考: 散布図に回帰直線を追加する)。どんな感じに引いても、さすがにこの散布図を線形回帰するのは無理があるだろうということも容易に推察できる。
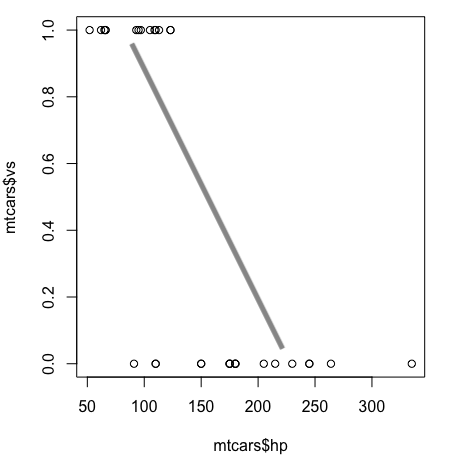
では、この散布図はどういう関数でモデル化すればいいだろうか。一般には log(p/1-p) = b0 + b1X という関数が使われる。これは 0 - 1 の範囲をとるシグモイド曲線の関数である。
下の図も手書きだが、イメージはこんな感じ。あとでちゃんとフィットさせる。
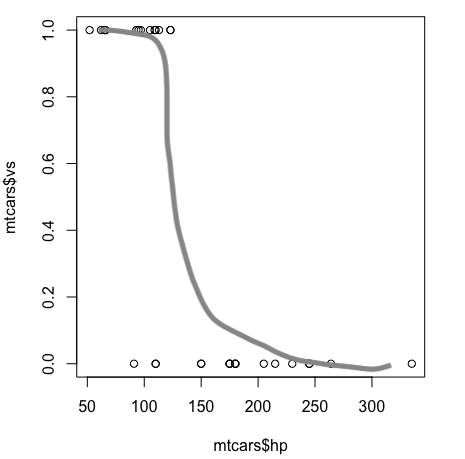
この形の関数を使うと、
この「確率の予測」がロジスティック回帰の主要なアウトプットである。
では、実際に回帰分析を実行してみよう。最初に述べたように family = binomial を指定する。

Estimate という部分が係数である。したがって、hp と vs の関係は次のように表すことができる。ただし、p は vs = 1 となる確率である。
log(p/1-p) = -0.06856hp + 8.37802
この関数をプロットしてみる。plot() でも可能 (4) だが、ggplot() の方が簡単そうである (参考: ggplot で散布図を作成する, 3)
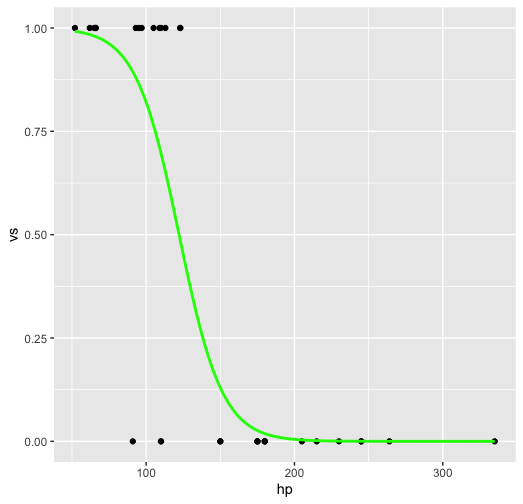
多変量のロジスティック回帰分析
複数の説明変数をモデルに入れたいときは、以下のように + で繋ぐ。

mpg, hp, wt を説明変数として使用した。hp のみが有意であることがわかる。なお、データセットにある全ての変数を含めたいときは . を使い、vs ~ . のようにする。
ロジスティック回帰では、log(p/1-p) = b0 + b1X1 + b2X2 + ... + bnXn という式がモデルとして使われる (2)。p は、注目した事象が起こる確率であり、変数が 0 or 1 ならば、「1 となる確率」のように解釈できる。1 - p は、「そうならない確率」である。したがって、「ある事象が起こる確率/起こらない確率」 (= オッズ比) の対数値が目的変数となる。
b0, b1, b2.... が計算される係数で、上の結果ならば
log(p/1-p) = 0.50291mpg - 0.09318hp + 3.87749wt - 10.61945
という式が成り立つことになる。
オッズへの変換と、フォレストプロットの作成
多変量の例を使って説明する。得られた式は、目的変数が対数値になっているので、ちょっと解釈が難しい。そこで、exp を使って左辺を単なるオッズにすることが行われる。なお、このオッズの対数値はその確率のロジット logit と呼ばれ、これはこれで重要な値である。
exp により、それぞれの説明変数の係数が以下のように変換される。棒グラフも表示しておいた。

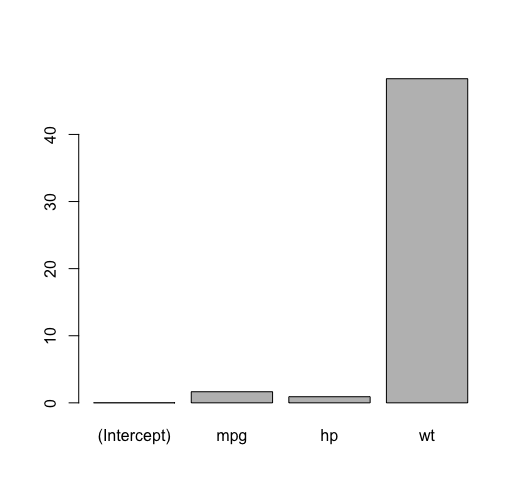
このことから、wt がもっとも vs = 1 である確率に影響を与えることがわかる。wt 以外の変数が全て同じとき、wt が 1 変化すると、vs = 1 である確率は約 48 倍に上昇すると解釈できる。wt と vs のプロットは以下のようになる。値が有意でないのに、これだけ影響が大きいというのはちょっと釈然としないが。
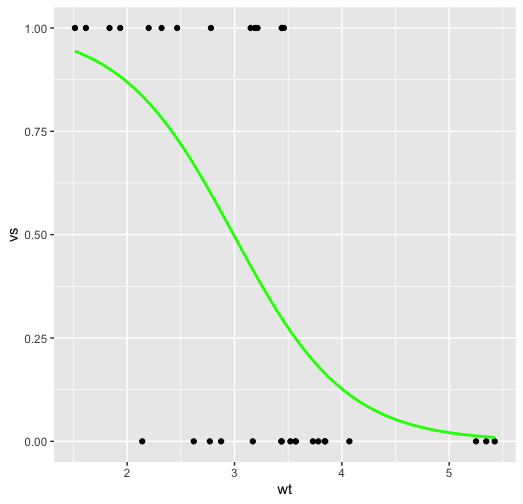
それぞれの要因をフォレストプロットで表示する (5)。plot_model() 関数に glm の結果を直接入れれば良いようである。
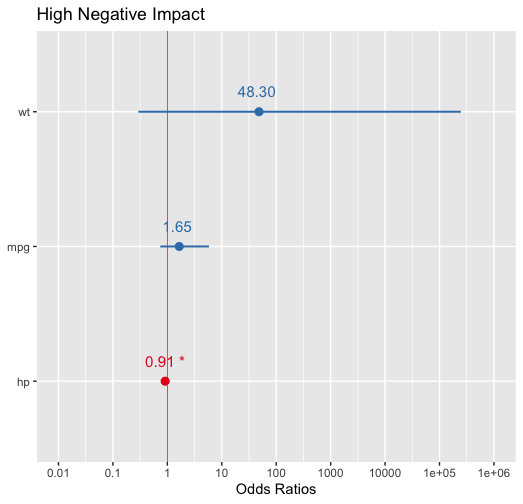
中央の赤いラインに重なっていなければ有意、赤線の左に行くほどオッズに対してマイナスの作用、つまり事象が起こる確率を下げる作用がある。
広告
References
- Rでロジスティック回帰分析 そのまま使える自作関数例. Link: Last access 2023/11/22.
- ”R”で実践する統計分析|回帰分析編:③ロジスティック回帰分析【外部寄稿】. Link: Last access 2023/11/22.
- How to Plot a Logistic Regression Curve in R? Link: Last access 2023/11/22.
- 生物統計学 ロジスティック回帰. Link: Last access 2023/11/22.
- Plotting Estimates (Fixed Effects) of Regression Models. Link: Last access 2023/11/22.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
