R: lm 関数による重回帰分析

このページの最終更新日: 2023/03/07

R による回帰分析

R では、回帰に以下のような基本関数が用意されている。このページでは、lm 関数を用いた回帰の方法、とくに説明変数が複数ある重回帰分析について説明する。

lsfit	最小二乗法による回帰線形回帰の手法のうち、回帰直線とデータの差 (誤差) を二乗して足し合わせた合計が最小になるような回帰直線を引く方法を最小二乗法という。最小二乗法は、関数を用いた近似には基本的に適用できる方法である。
lm	線形モデルによる回帰
glm	一般線形モデルによる回帰
nls	Nonlinear least squares の略。関数を定義して非線形の回帰を行う場合に使う (参考ページ)。最小二乗法を使っている。

以下のような関連ページもあるので参照のこと。

線形重回帰では、複数の変数 X を使って Y を予測する。やはり swiss にある出生率 Fertility を Y とし、これを 2 つの変数 Examination と Education がどの程度説明するかを調べてみる。

なお、Examination 変数の 47% が Education で有意に説明されるという結果が得られているため、この 2 つを変数として含めると、多重共線性 multicollinearity という問題が生じる。しかし、とりあえず手法を学ぶ目的で重回帰をやってよう。

単回帰と同様に lm 関数を使う。

lm の結果をオブジェクトとして保存する。複数の x がある場合、lm の基本形は lm(y ~ x1 + x2) である。+ を使っていくらでも x を増やせる。
そのオブジェクトの詳細を summary 関数で表示する。

具体的なスクリプトは以下の通り。ただし、多くの場合は変数間の交互作用も確認したいので、ページ下の「交互作用がある場合」のように + でなく * を使うべきだろう。

sfee = lm(swiss$Fertility ~ swiss$Education + swiss$Education)
summary(sfee)

結果は次のようになる。Examination, Education ともに有意であり、この回帰は出生率の 48% を説明する。回帰式は

出生率 = -0.5572 * Examination - 0.5395 * Education + 85.2533

である。なお、例えば切片が有意でなかった場合、回帰式には切片を含めないことになる。

また、重回帰分析においても与えられる決定係数 R² は一つだけであり、これはモデリングの全体的なフィットの良さを示す値になる。どの変数がどれだけフィットしているかという情報は得られない。

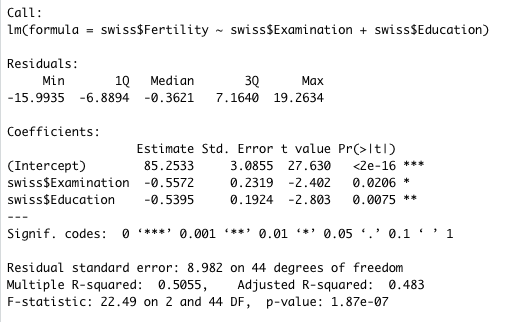
なお、上の書き方では swiss をいちいち指定しているが、これは面倒なので、以下のようにデータをまとめて指定することができる。こちらの方がよく使われるかもしれない。

sfee = lm(Fertility ~ Examination + Education, data = swiss)

一方、Education と Examination の交互作用を見たい場合は、+ の代わりに * を用いる。同じデータで分析すると、このようになる。

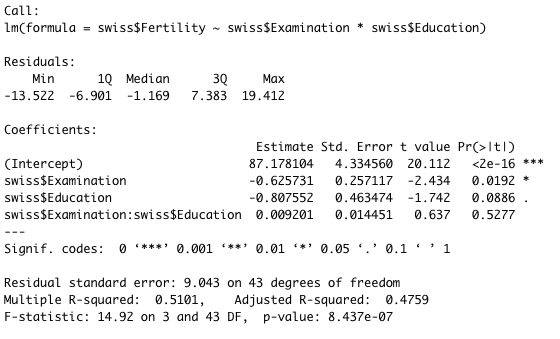
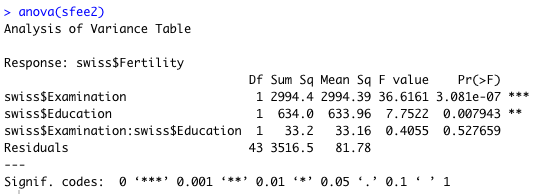
これを ANOVA に入れると、以下のようなパラメーターを見ることができる。

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。