1. 概要: 生存時間分析とは
2. Kaplan-Meier survival curve
   • 累積生存率のプロット
   • グラフの解釈
   • 累積死亡率のプロット
3. 生存曲線が交差する場合
4. 臨床試験: 生存時間は「いつから」？

概要: 生存時間分析とは

生存時間分析 survival analysis とは、ある イベントが起きるまでの時間と、イベントの間の関係 に焦点をあてる分析方法である (1)。イベントを死亡と考えると、寿命を分析する方法になる。また、工学分野では機械の故障などをイベントと考え、製品の分析にこの方法が使われている。

イベントが生じるまでの時間 T を生存時間とよび、T は確率を自らの要素としてもっている数、すなわち確率変数 random variable である。

生存時間 T は、一般に正規分布 normal distribution には従わず、以下のような分布に従う (4)。

• Exponential distribution
• Weibull distribution
• Lognormal distribution

したがって、平均寿命を t 検定 などのパラメトリック検定で比較するのは正しくない。ノンパラメトリックな Mann-Whitney の U 検定 で比較することは間違いではないが、生存時間分析のデータに特徴的な 打ち切り censoring を考えると、U 検定もベストの方法とは言えない。

打ち切り censoring

たとえば、ある病院における患者の死亡をイベントとしたデータをとっている最中に、患者が転院していなくなった場合には、死亡とみなしたり、そのデータを除外したりするのではなく、右側打ち切り right censored として記録する。これは、「正確な survival time は不明だが、ある時間以上生存していたことはわかっている状態」である (4)。

打ち切り censoring は生存時間分析において重要な概念であり、これを統計的に処理できることが生存時間分析の利点の一つである。

生存曲線 Survival curve: Kaplan-Meier 法

累積生存率のプロット

生存時間分析に供するデータは、図 (Public domain) のように表すのが最も一般的であり、これは Kaplan-Meier survival curve と呼ばれる (4,5)。

この方法は、縦軸に累積生存率を、横軸に時間をとったもので、生存データを視覚的に把握することができる。

ポイントは、生存率を斜めに繋ぐのではなく、階段状の図ができるように繋ぐことである。

また、打ち切りが生じた場合には生存曲線に短い縦線を入れて表すこともある。

一方、Kaplan-Meier method という言葉もある。これは、上の生存曲線のグラフに現れている Kaplan-Meier の考え方を示す言葉と捉えて良さそうである (7)。

• Non-parametric な生存時間の推定法。つまり、生存時間が特定の関数で表されると考える Hazard function 法とは異なる。
• 関数を仮定しないので、データ (生存時間と打ち切り) のみが生存時間を算出する根拠となる。このために、データをわかりやすく表現する生存曲線が描かれるわけである。
• 欠点として Mainly descriptive, Doesn't control for covariates, Requires categorical predictors, Can't accommodate time-dependent variables の 4 つが挙げられている (7)。

グラフの解釈

Kaplan-Meier のグラフを解釈する際には、次のような点に注意する必要がある。

> 生存期間の中央値 は、生存期間の目安の一つである (5)。

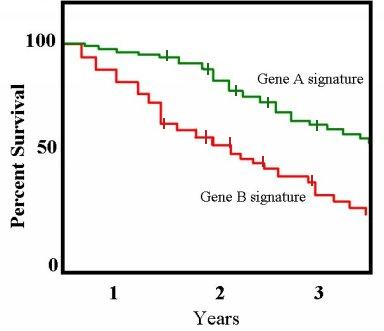
• 50 % survival rate から横に延ばした線が生存曲線と交わる点がこれにあたる。

> 右の方に行くほど サンプル数 N が少なくなるため、生存曲線の精度が下がる (5)。

• 上の図で、最後に Gene A と Gene B が逆転していたとしても、その意味はあまり大きくない。
• Kaplan-Meier は、あくまで 生存曲線全体を比べる ためのものである。

累積死亡率のプロット

縦軸に累積死亡率をプロットすると、ちょうど累積生存率のプロットの裏返しの右上がりの図ができる。これも Kaplan-Meier と呼ばれる (5)。

生存曲線が交差する場合

生存曲線が交差するということは、瞬間生存率が交差している時点の前後で異なることを意味する。したがって、瞬間生存率が一定であることを仮定する比例ハザードモデル (Cox 回帰モデル) および Log-rank test を使えないので注意が必要である。

> 生存曲線が交差する場合には、統計検定をかける上で注意が必要である (6)。

• 瞬間生存率が交差している時点の前後で異なることを意味する。
• 瞬間生存率が一定であることを仮定する比例ハザードモデル (Cox 回帰モデル) が使えないので注意。
• Log-rank test も proportional hazard を仮定しているので使えない、と書かれている (8)。

> Simulation study (9). Adaptive Neyman's smooth test が良いとする。

• 文献調査、survival analysis を行っている論文の 47% が crossing survival curve.
• しかし、その 70% が log-rank test を使用、そのうち 31% しか proportional hazards を調べていない。

臨床試験: 生存時間は「いつから」？

動物実験の場合には、上の図のように出生時を起算日 time 0 として生存曲線を解析することができる。しかし、生存期間を評価する臨床研究では、以下の 4 つを起算日にすることが可能である (5)。

疾患が発生した時点

明瞭な自覚症状がある疾患では可能であるが、糖尿病やがんなどでは難しい (5)。

診断日

診療記録から明確に定めることができるが、患者によって疾患の進行状況が異なる可能性がある (5)。

ランダム化 (割り付け) 実施時点

ランダム化比較試験の場合、症例登録を行い、治療法の割り付けを行った時点を起算日とするのが通例である(5)。

治療開始時点

治療の効果に主眼を置いた研究では、これも妥当かもしれないと書かれている (5)。

References

1. R と生存時間分析. リンク切れ.
2. 汪 2005a. 生存時間解析入門. pdf file.
3. Survival Analysis in R. Link: Last access 2020/06/08.
4. JMP Statistics and Graphics Guide. SAM, 2007.
5. 佐藤弘樹、市川度. 2013.

6. 生存曲線が交差する場合. Yahoo 知恵袋. Link.
7. Sainani K. Introduction to Survival Analysis. Stanford University.
8. Survival analysis. リンク切れ.
9. Li et al. 2014a. Statistical inference methods for two crossing survival curves: a comparison of methods. PLoS ONE 10, e0116774.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。