生存時間分析 - Log rank 検定:
UB3/statistics/survival/log_rank
このページの最終更新日: 2025/11/23関連ページ
広告
概要: Log-rant test とは
Log-rant test とは、ある時点の生存率でなく、
生存時間 T は、一般に正規分布 normal distribution には従わず、exponential distribution, Weibull distribution, Lognormal distribution などの分布に従う (4)。したがって、寿命を t 検定などのパラメトリック検定で比較するのは正しくなく、Log-rank 検定などの専用の検定が必要となる。
Log-rank 検定の基本的な考え方は、カイ二乗検定 chi-square test に似ているようである (5)。
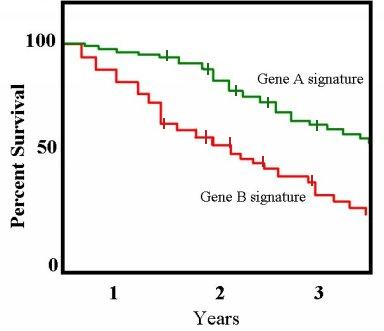
- 右図の生存曲線 (3) である時点 t1 を選び、そこで n 件の死亡が起こったとする。
- 例えば図で 2 年の時点を考えると、個体数はおよそ A : B = 1.5 : 1 であるため、n 件の死亡のうち 1.5/2.5 は A 群で、1/2.5 は B 群で起こると予想される。
- ただし、これは両群の死亡率 (つまり生存期間) に差が無い状態であり、実際にはこの割合から微妙にずれて死亡というイベントが起こっているわけである。
生存曲線全体にわたって、この「ずれ」 の具合を検定する のが Log-rank 検定である。
生存数と死亡数のデータを使って、カイ二乗検定・独立性の検定で比較する場合もあるが、これは一点の生存数データしか使っていないことになる。
つまり、上のグラフのエンドポイント (3 年の観察期間終了後) のデータで統計検定を行う場合、カイ二乗検定 では 1 年目の死亡と 3 年目の死亡を同じものとして考えてしまう。したがって、log-rank 検定の方が適した解析手法と言える。カイ二乗検定・独立性の検定 にも関連する記述があるので参照のこと。
広告
群が複数あるときの Log-rank 検定
Log-rank 検定は、基本的に
生存曲線が交差する場合
Log-rank test は、proportional hazard rates を仮定した場合に、最適な power を与える検定である (9)。
生存曲線が交差するということは、瞬間生存率が交差している時点の前後で異なることを意味する。したがって、瞬間生存率が一定であることを仮定する Log-rank test を使えないので注意が必要である。詳細は 生存曲線 のページに。
広告
References
ページ編集のため番号が飛んでいますが、本文の内容とは対応しています。
- ページ編集に伴い削除
- ページ編集に伴い削除
- "Km plot" by Deanne Taylor (made and original to submitter) - Transferred from en.wikipedia to Commons by Maksim. The original description page was here. All following user names refer to en.wikipedia.. Licensed under Public Domain via Wikimedia Commons.
- JMP Statistics and Graphics Guide. SAM, 2007.
佐藤弘樹、市川度. 2013.
|
生存時間解析 について平易に書いた数少ない解説書。 統計のなかでも、生存時間解析はそれだけで 1 冊の本になるほど複雑なわりに、ANOVAや t 検定などと違い使用頻度が低いため、とっつきにくい検定である。 この本では、とくに |
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
