1. 概要: Cox ハザードモデルとは
2. ハザードとは

概要: Cox ハザードモデルとは

図のような生存時間のデータがあるとき、log-rank 検定 を使うことで、生存率の差を生存曲線全体にわたって比較することができる。

赤と青の群で、サンプルの背景 (性別、年齢など) が揃えられていれば、log-rank 検定で問題はない。しかし、ヒトを対象とした臨床試験の場合、背景を一致させることは難しいので、データ解析の段階でこれらの影響を調整する必要が生じる。

Cox ハザードモデルは、これらの影響を考慮しつつ、生存時間データを解析するためのモデルである (1)。

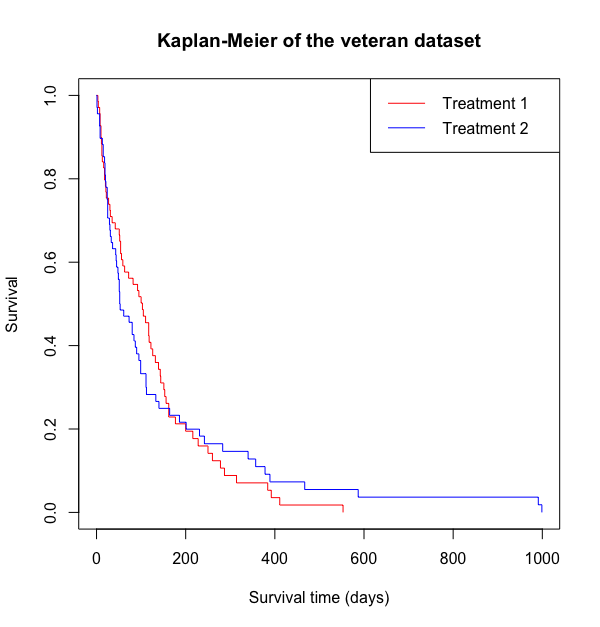
実験生物学では、基本的に実験動物の背景を揃えた上で実験を行い、結果を比較する。したがって Cox ハザードモデルが登場する機会は少ない。これは原則として臨床統計分野の手法である。また、さまざまな要因をモデルに加える 回帰分析 の一種である。

Cox 回帰モデル、比例ハザードモデルとも呼ばれる。ハザードの比が一定であることを仮定したモデルである。

ハザードとは

Cox ハザードモデルでは、生存期間や生存割合でなく、ハザード という概念を使ってモデルと作る。

ハザードは、ある時点の瞬間における死亡率 を表し、単位は一般に "人/単位時間" である。時間によって変動する。

たとえば、3 か月目のハザードは、「3 か月目の直前まで生存していた被験者が、3 か月目の瞬間に死亡する確率」である。

Cox ハザードモデルでは、時間とともに変動する「基準ハザード」があり、これに背景が加わって「ある時点におけるハザード」になると考える (1)。

式 1:
ある時点のハザード =
基準ハザード + 背景 (性別、年齢など) + 介入 (治療など) の効果

さらに、以下の仮定をおく。

1. 基準ハザードは時間とともに変化するが、背景の効果は一定である。
2. 群が異なっても、時点が同じであれば、基準ハザードは同じである。

ここで、介入の効果を Cox ハザードモデルで求めたいとしよう。

まず、ハザードは実際の生存データから計算することができる。

基準ハザードは、介入の効果がわからないために不明である (式 1)。しかし、2 つの群のハザードがあれば、それらの比をとることで基準ハザードを約分して消去できる (仮定 2)。

したがって、介入効果の比が、ハザードの比として推定できることになる。

References

1. 佐藤弘樹、市川度. 2013.

2. オッズ比とハザード比：似て全く非なるものーその2. Link: Last access 2022/10/09.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。