回帰分析の概要
UB3/statistics/correlation/regression_overview
このページの最終更新日: 2025/11/23広告
回帰分析 regression analysis とは
このページは、回帰分析 regression analysis の概要を説明するためのページである。
回帰とは
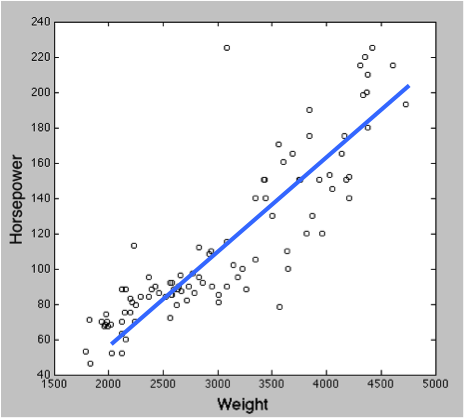
- 通常は、変数 X によって変数 Y の変化を予測することになる。x が一つならば単回帰分析、複数ならば重回帰分析である。
- 青い直線を示す式が X と Y の関係性を表すことになる。これが y = ax + b のような一次式なら、線形回帰分析と呼ばれる。
X と Y はさまざまな名前で呼ばれる。
X は独立変数 independent variable のほか、説明変数 explanatory variable、予測変数 predictor variable とも呼ばれる。連続変数であることが一般的だが、名義尺度 しか持たないカテゴリー変数でも OK。
Y は応答変数 response variable (目的変数、反応変数) という名前のほか、従属変数 dependent variable、基準変数 criterion variable、非説明変数 explained variable とも呼ばれる。
回帰分析の目的
回帰分析に似た統計手法に、相関分析 correlation analysis がある。
相関関係と因果関係の対応から、なんとなく相関分析は相関関係を調べるもので、回帰分析は因果関係を調べるもののような印象を持ってしまうが、
回帰分析は様々な目的に使われるのでややこしい。まず目的を意識し、それに合った使い方と議論をしなければならない。私の理解では、回帰分析は少なくとも以下の 3 つの目的で使うことができる。
予測 |
予測精度のみを問題にするというアプローチ。この目的で行う場合、交絡 confounding、多重共線性、各回帰係数が有意であるかどうかは、原則として問題にならない。 |
説明 |
中途半端な立場で、予測と言っておきながら因果についても議論したい場合。機械学習系の人は認めない傾向がある。 |
因果推論 |
因果関係まで議論したい場合。サンプルの取り方から検討する必要がある。 |
因果推論 Causal inference
A と B に相関があるとする。これは A → B という因果関係とは異なるが、実際に知りたいのは因果関係である場合が多い。因果関係を証明するには、コントロールをとる必要があるが、実はコントロールにもいくつかの種類がある。
理想だが不可能 |
「全く同じ条件 (同一個体、同一条件)」において、A があるときに B、A がないときに C という結果が得られたら、B と C の違いが A で説明できる (A が原因である) ことになる。 タイムマシンを使ったり、完全に同一のパラレルワールドを行き来できたりする場合にのみ可能になる。 |
ランダム化比較実験 |
Randomized Controlled Trial (RCT) と呼ばれる。一般的な生物学的実験の手法だろう。グループを使って比較する。 グループ 1 には条件 A として薬などを与え (「介入」と呼ばれる)、その結果として B というデータが得られる。 グループ 2 には条件 A を与えず、C という結果がえられる。グループ 1 と 2 が十分にランダム化されている (均質とみなせる) 場合、A が原因であると言える。問題は、グループ 1 と 2 が本当にランダム化されているかどうか確認する手法がないことである。 |
回帰不連続デザイン |
Regression discontinuity (RD) デザイン。2 つのグループを作って実験をするわけでなく、既存のデータを分析する手法。自然に介入が発生したとして、その前後を比較する。 |
参考ページ。
機械学習と統計の違い
機械学習は予測精度を追求、統計は解釈にも興味。しかし両者は大きく重なる、というのが現時点での理解。人工知能の概要 のページなどを参照のこと。
広告
様々なタイプの回帰分析
考えるべきポイントはいくつかある。
- 説明変数 X の数 – 単回帰とか重回帰という表現になる。
- 回帰式の次数 - 一次なら線形回帰 (Y = aX + b の形)、それ以上だと非線形回帰。
- 最適な回帰式を求める方法 - 最小二乗法、主成分回帰、正則化回帰など、それぞれの手法に応じた名前がつくことが多い。
線形単回帰 |
Y = aX + b というシンプルな回帰。 線形回帰を行うにはいくつかの条件があり、それを判定する方法もある (参考)。 R の lm 関数による回帰分析 に、線形の単回帰および重回帰の方法が書かれている。 |
Y = aX1 + bX2... のように、複数の説明変数 X を利用した回帰。Multiple regression。線形も非線形も可能である。 X をいくつまで含められるかは当然ケースバイケースであるが、回帰分析: データ数および因子数は何個まで含められるのか のページに詳細をまとめた。 説明因子の間に相関があると、多重共線性といって回帰係数が大きく不安定になる問題が生じる。 |
|
非線形回帰 |
説明変数の数でなく、フィットする関数による言い方である。R では nls 関数を用いる。まず数式を指定してから、データを指定。どのモデルにあてはめるか、どのような値を初期値とするかは、データ解析者の経験と勘に頼るものらしい (参考)。 |
SMA 回帰 |
シンプルな線形単回帰が適当でない場合には、II 型の回帰分析というものがある (Ref)。Standard major axis regression (SMA) または reduced major axis regression (RMA) とも呼ばれる。線形回帰は X や Y に誤差がある場合には適当でなく、X と Y の両方が測定値である場合などには II 型が適している。 |
ロジスティック回帰 |
応答変数 Y がカテゴリー変数の場合、ロジスティック回帰と呼ばれる。 Y が A であるか否か (つまり Y = A が TRUE か FALSE か) を説明しようとする分析である。参考: R glm() 関数を用いたロジスティック回帰 |
主成分回帰 PCR |
主成分分析 のようなアイディア。説明変数 X の数が多い場合、それらを主成分に変換して回帰する。主成分は互いに独立なので、多重共線性の問題は生じない。 複数の X を扱うので、重回帰の一種と言える。 |
部分最小二乗回帰 PLS |
説明変数を互いに独立な潜在変数に投影し、それらを回帰する。これも重回帰の一種である。 |
上の 2 つ (PCR, PLS) は説明変数を減らすための手法であるが、正則化回帰は同じ問題に説明変数を減らさずに対処する。データにノイズを入れて overfitting を回避しつつ、回帰係数が大きくなることに対してペナルティを与える。詳細はリンク先を参照のこと。 |
|
複数のレベルで変化するパラメータに対する統計モデル。たとえば、サンプルが全体として負の相関を示しているが、実はサンプルはいくつかのグループから構成されており、グループごとに相関が異なる場合などは、マルチレベル分析が適している。 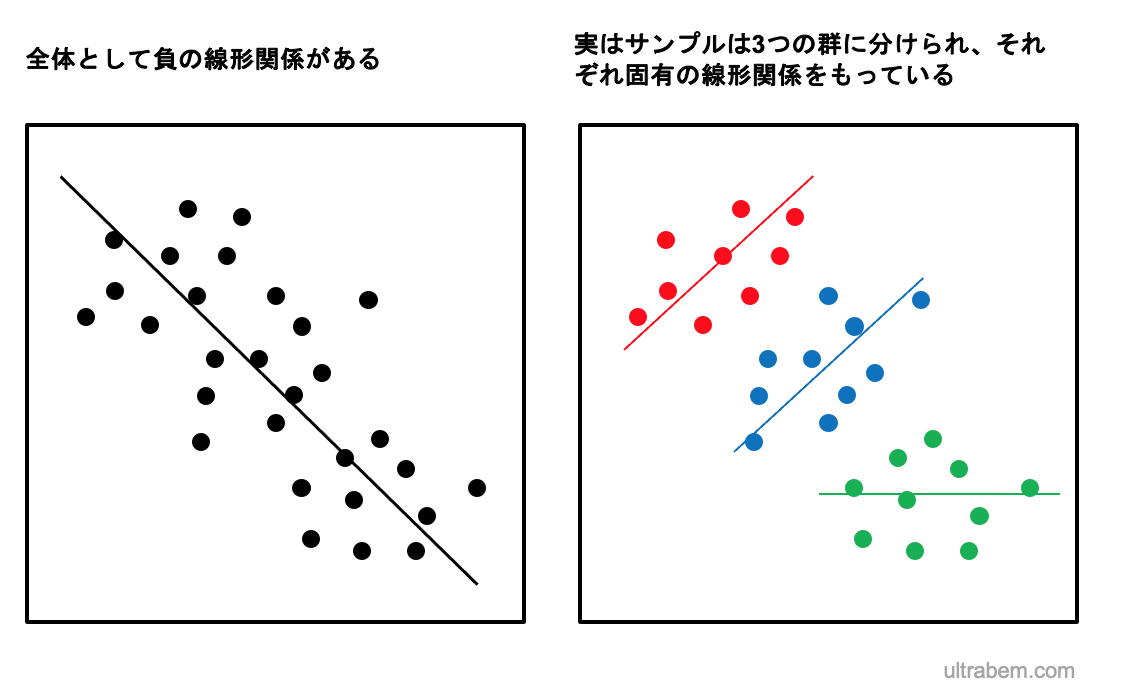
|
その他、重要な用語。
- 交差検証 cross-validation: 交差確認とも言う。標本データを分割し、まずその一部を解析。残る部分でその妥当性を検証するという手法を意味する。
広告
References
- 臨床統計 まるごと図解.
|
生存時間解析 について平易に書いた数少ない解説書。 統計のなかでも、生存時間解析はそれだけで 1 冊の本になるほど複雑なわりに、ANOVAや t 検定などと違い使用頻度が低いため、とっつきにくい検定である。 この本では、とくに |
- What is the purpose of regression analysis? Link: Last access 2020/06/29.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
