交絡 confounding とは:
定義、交絡作用と交互作用の違いなど
UB3/statistics/correlation/confounding
このページの最終更新日: 2025/11/23広告
概要: 交絡 confounding とは
交絡 confounding とは、要因 factor と結果 outcome の両方に影響を与える因子があり、そのために両者の関係を正しく理解できなくなる現象をいう。その因子を交絡因子という。
たとえば、以下の図である。アルコール摂取量が増える (要因) と、ガンのリスクが上がる (結果) という論を立てていたが、実は「年齢」という交絡因子があり、つまり「老人ほど酒を飲み、ガンにかかりやすいだけ」だったということ。
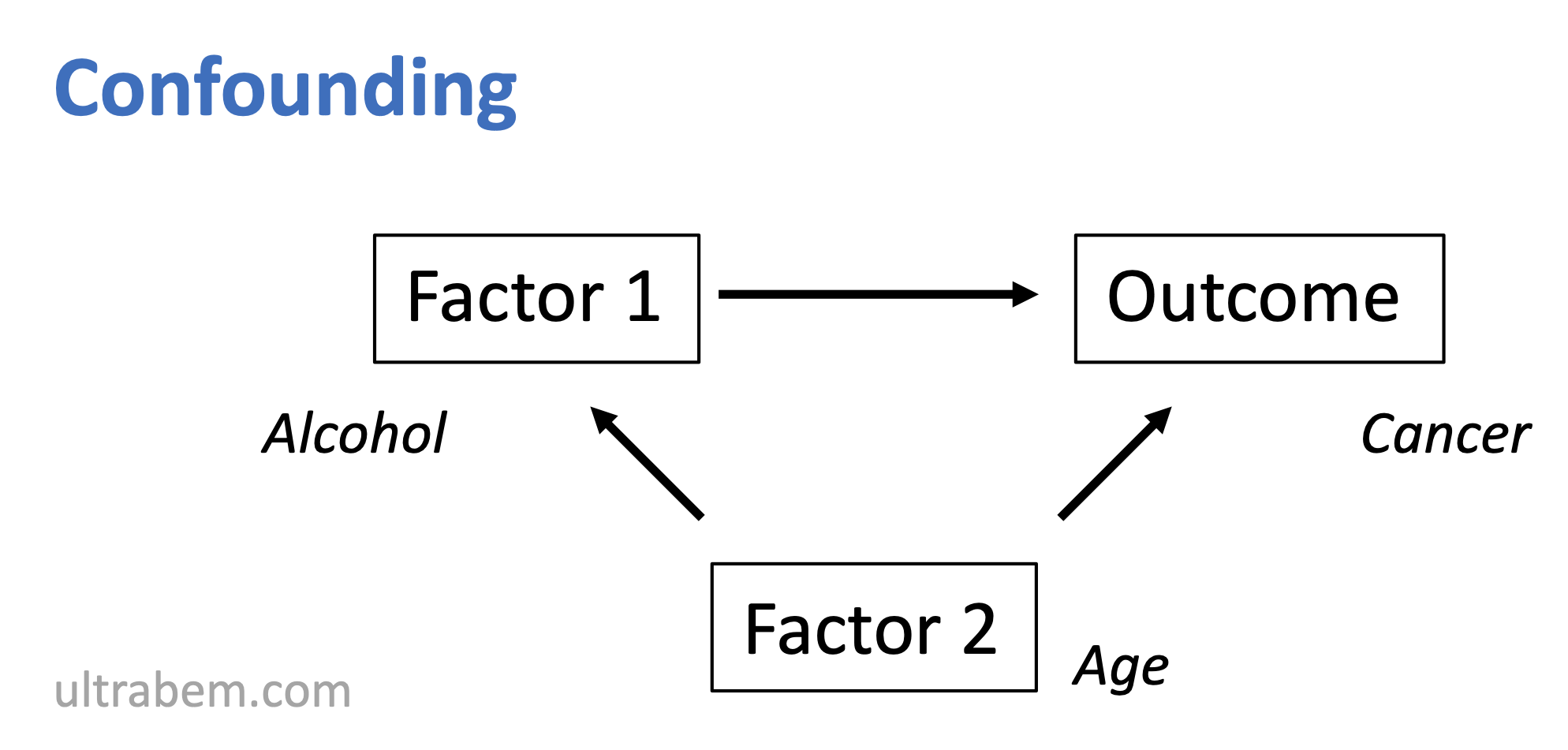
いくつか定義を載せておく。
- 治療と、それによってもたらされる結果 (アウトカム) の関係を評価する際に、治療の選択と関連があり、かつアウトカムにも影響を与える因子があると、治療とアウトカムの関係を正しく評価できなくなる。この現象を交絡といい、それを起こす因子を交絡因子という (2)。
交絡因子は、以下のような名前でも呼ばれる。
- 交絡因子 confounding factor
- 交絡変数 confounding variable
- 共変数 covariable
交絡因子の影響を考慮して、目的のデータを総合的に比較するのが 共分散分析 ANCOVA である。ANCOVA では共変数 covariance という言葉が使われることが多いようである。
アイスクリームと水難事故のように、相関関係を説明する因子とする説明もあるが、「治療とアウトカム」のような因果関係を想定している場合を例として説明されている場合が多い。
交絡の例
> アルコール、喫煙、肺ガンを例としたわかりやすいページ (1)。
- ある調査の結果、アルコール摂取量と肺ガンのリスクに相関があったとする。
- アルコール摂取が肺ガンの原因とするのは短絡的な解釈。たとえば、アルコールを飲む人はタバコもたくさん吸う傾向にある。よって、実際にはタバコが肺ガンの原因かもしれない。
- この疑問点を解決するには、タバコを吸う人と吸わない人に分けて調査すればよい。これを
層別化 という。 - 層別化によってアルコールと肺ガンの関係が観察されなくなれば、タバコが交絡因子である。
- アルコール自体にも肺ガンとの相関があれば、アルコールとタバコは独立に、または交互作用しながら肺ガンのリスク因子となっている。
交絡と交互作用の違い
図に示したように、ポイントは要因 2 が要因 1 に直接影響を及ぼすのが交絡、要因 1 の 結果への作用に影響を及ぼすのが交互作用である。英語の "effect modification" の方がわかりやすい。まさに effect のみを modify しているのである。
図の交互作用を、適当な数字を使って説明してみよう。
- アルコールはガンのリスクを 10% 上げる。
- 喫煙自体もガンのリスクを 10% 上げるが、アルコール + 喫煙で、ガンのリスクが 30% 上がる。単なる相加的な効果以上の効果があるということ。
- 喫煙がガンのリスクを上げるかどうかは問題でない。図では、喫煙自体はガンのリスクを上げない (0% なので、smoking から outcome への矢印がない) が、喫煙 + アルコールは、アルコールのみ以上にガンのリスクがあがるという状況。
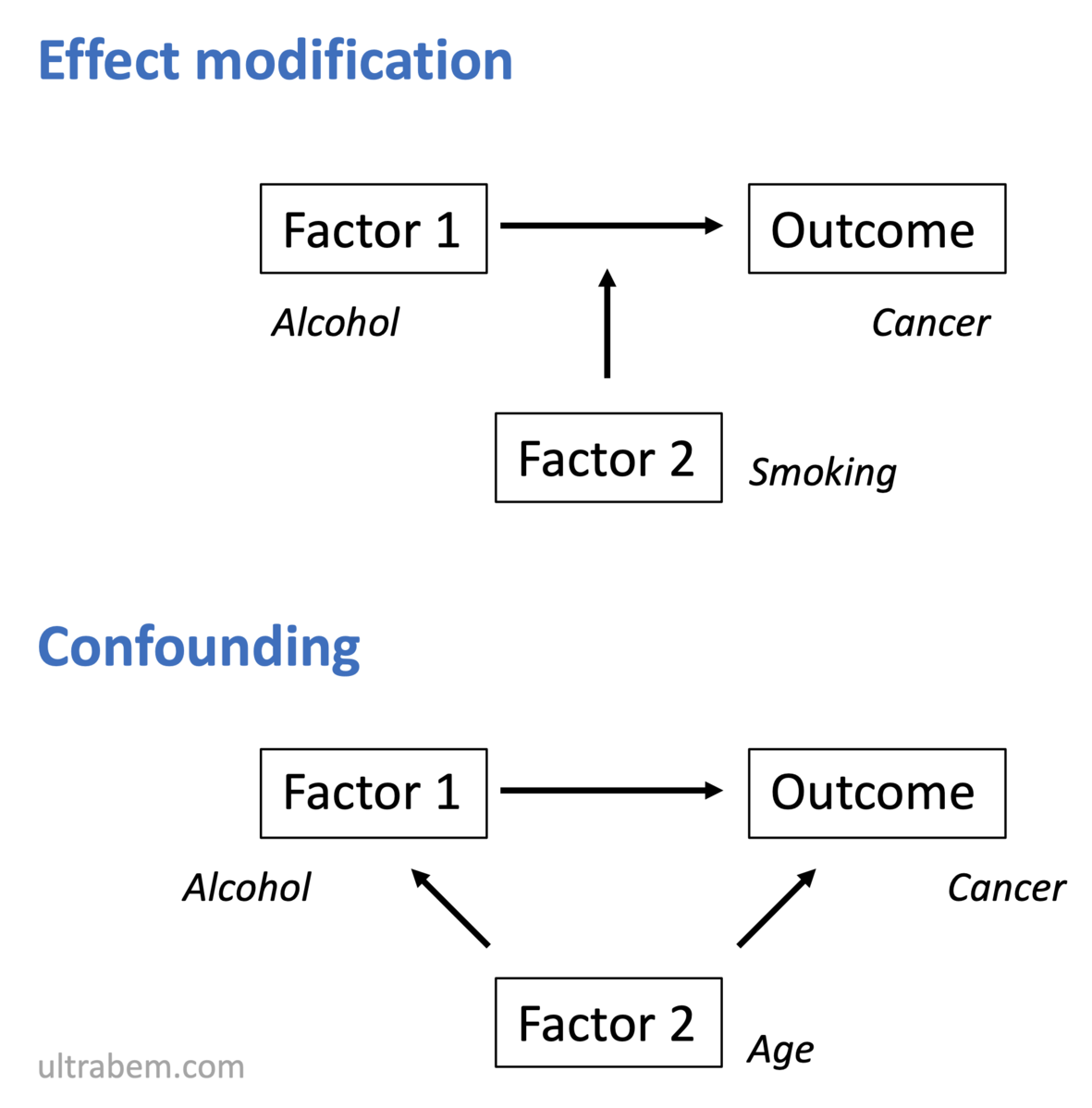
交互作用と交絡はこのように異なるものであるが、排他的な概念ではない。たとえば smoking が飲酒率を上げ、ガンのリスクを上げ、さらに飲酒によるガンのリスク上昇に対して交互作用を示すならば、それは
交絡がある場合にどうするか
実験系の生物学では、実験の計画を立てる際に (場合によっては無意識に) 交絡因子を排除していることが多い。オスの個体のみを使う、齢や体重を実験開始前に揃えるなど、サンプルの取り方によってかなりの潜在的な交絡因子を排除できる。
よって、交絡は実験生物学ではなく医療でよく使われる概念である。
ランダム化
治療法の選択を、患者の状態や医師の判断によらずランダムに割り当てる (2)。単純ランダム化、層別ランダム化、ブロックランダム化など複数の方法がある。
共分散分析
交絡因子を説明変数に加えて、多変量解析を行う (3)。
文献 5 では、説明変数と従属変数の間に交絡がある場合について述べている。
広告
References
- 【医学統計勉強メモ】交絡Confoundingと交互作用Effect modification.Link: Last access 2020/05/08.
- 臨床統計 まるごと図解.
|
生存時間解析 について平易に書いた数少ない解説書。 統計のなかでも、生存時間解析はそれだけで 1 冊の本になるほど複雑なわりに、ANOVAや t 検定などと違い使用頻度が低いため、とっつきにくい検定である。 この本では、とくに |
- 交絡因子とは.Link: Last access 2020/05/09.
- 回帰分析 その1:回帰分析で交絡因子の影響を取り除く.Link: Last access 2020/06/18.
- 回帰分析における「調整変数」の選び方:実践編. Link: Last access 2025/11/21.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
