1. 概要: マルチレベル分析とは
2. マルチレベル分析を行うべきデータの構造
3. ICC および Deff

概要: マルチレベル分析とは

マルチレベル分析 multilevel analysis とは、マルチレベルモデル multilevel model (MLM) を使った分析のことをいう。

なぜか、「マルチレベルモデル」という言葉に関する解説の方を多く見る気がする。このモデルは 階層線形モデル hierarchial linear model (HLM) とも呼ばれ、個人的にはこの呼び方の方がしっくりくる。

マルチレベル分析は、回帰分析 regression analysis の一種である。実際の例をみてみるのがわかりやすいだろう。

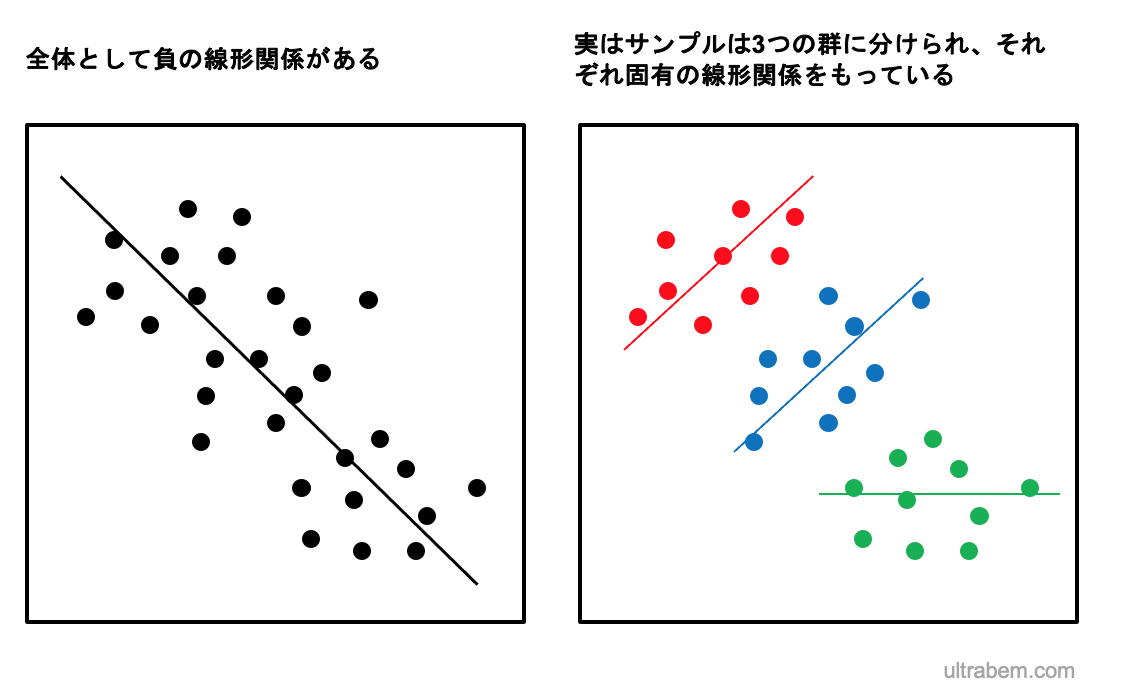
この図 (Public domain) の左側にあるように、X と Y の間には負の相関関係があり、両者の関係は負の線形関数で表すことができる。

ところが、図の右側のように、このサンプルは実は赤・青・緑の 3 つの群に分かれており、別々に分析した場合、赤と青では正の相関、緑では相関なしであった。

データの分布は全く同じであるにも関わらず、グループごとに解析するだけでこのように非常に異なる結果が得られるのは興味深い。このようなグループ分けと異なるモデルの適用が、マルチレベル分析の基本的な考え方である。

マルチレベル分析を行うべきデータの構造

キーワードは nested である。日本語では「入れ子構造」などと呼ばれる。つまり、データが一つの集団に属するのではなく、上位構造に入っている場合には、マルチレベル分析を考える必要がある。

• 上の図の例では、データは赤・青・緑というグループにネストされていることになる。
• 児童・生徒を対象とした教育関係の論文では、児童・生徒がクラス・学校・地域という複数のカテゴリーにネストされている (1)。したがって、教育学の論文ではマルチレベル分析は頻繁に用いられる。同じ介入をした場合でも、その影響がクラス・学校・地域によって異なるかもしれないためである。
• 同様に、医学研究でも医者・病院・地域などに患者がネストされているという構造になる。同じ薬を使っても、医者・患者・病院によって結果が異なるかもしれないため、マルチレベル分析を検討すべきである。

ICC および Deff

マルチレベル分析を行う必要があるかどうかを決める指標として、級内相関係数 (ICC: intra-class correlation coefficient) がある。

ICC は、「結果変数の分散のうち、集団が締める分散の割合を示すもの (2)」である。データが集団に依存せず、完全に個人に依存している場合、ICC = 0 となる。また、データが 100% 個人の属する集団で決まる場合、ICC = 1 となる。

一応の目安として、ICC が有意で、0.1 を超えている場合、マルチレベル分析が推奨されると書かれている (2)。

References

1. 知っておきたいマルチレベル分析の考え方. The Annual Report of Educational Psychology in Japan, 48, 60-63, 2009.
2. 小川, 2019a. マルチレベル分析の特徴と HRM 研究に関するレビュー ─ HLM を中心に. 日本労働研究雑誌, 705, 35-40.

   コメント欄

   サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。