相関分析と回帰分析の違い
UB3/statistics/correlation/correlation_regression
このページの最終更新日: 2025/11/23このページは、相関分析および回帰分析に関する内容の導入的なページです。
広告
概要: 相関分析と回帰分析の違い
相関分析 correlation analysis と回帰分析 regression analysis は、どちらの場合も右上がりの散布図がよく使われ、混同しやすい分析である。しかし、両者は明確に異なるものなので、しっかり区別しなければならない。
変数 x と y がある場合、相関分析と回帰分析は次のように異なる。
- 相関分析は 2 つの変数 x と y がどれくらい関係しているかを調べる分析である。-1 から +1 の間の値をとる
相関係数 を算出する (1)。 - 回帰分析は、ある変数 x からもう一つの変数 y の変化を計算するための分析である。
x と y の関係式を算出する 。グラフに線を引くのは回帰分析である。
相関分析、回帰分析とも、まずは両変数の散布図を作成するのが第一歩である。
相関分析とは
相関 correlation には、変数が 正規分布 することを想定したパラメトリックな相関と、正規分布を想定しないノンパラメトリックな相関がある。
パラメトリックな相関では、
- 強い相関と弱い相関があり、その強さは -1 から +1 の間の値をとる相関係数 ρ で表される。相関分析で得られるのは、この無次元の ρ であり、式で表されるような直線は得られない。
- 右上がりの正の相関 (0 < ρ < 1) と、右下がりの負の相関 (-1 < ρ < 0) がある。相関係数 ρ の符号が相関の正負を示す。
- 2 つの変数の間に因果関係を想定してはいけない。
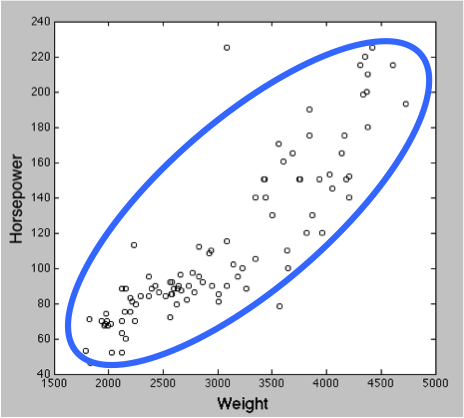
青い円の大きさが相関の程度を示すことになる。楕円が細長くなっているほど、相関係数の絶対値は一般に大きくなる。
ノンパラメトリックな相関分析には、スピアマンの相関 Spearman's correlation またはケンドール・タウの相関検定 (参考ページ) がある。
変数の分布によっては対数変換をすることがあるが、スピアマンの相関は順序だけが考慮されているので、対数変換しても全く同じ相関係数が算出される。
広告
回帰分析 regression analysis とは
回帰分析とは
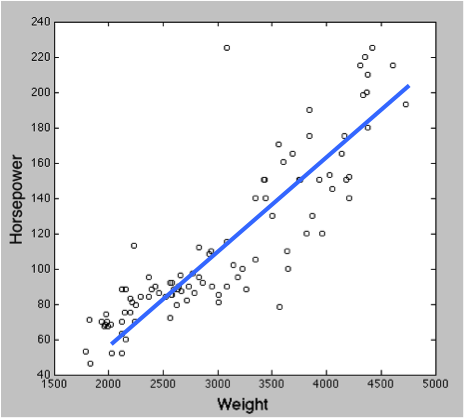
- 通常は、変数 x によって変数 y の変化を予測することになる。x が一つならば単回帰分析、複数ならば重回帰分析である。
- 青い直線を示す式が x と y の関係性を表すことになる。
x と y はさまざまな名前で呼ばれる。
x は独立変数 independent variable のほか、説明変数 explanatory variable、予測変数 predictor variable とも呼ばれる。連続変数であることが一般的だが、名義尺度 しか持たないカテゴリー変数でも OK。
y は応答変数 response variable (目的変数、反応変数) という名前のほか、従属変数 dependent variable、基準変数 criterion variable、非説明変数 explained variable とも呼ばれる。
y が 0 と 1 しかない二値変数の場合にはロジスティック回帰になる (参考: R glm() 関数によるロジスティック回帰)。たとえば、血液のパラメーター、体重などから、被験者が病気である = 1、病気でない = 0 などを予測するような場合である。
相関関係と因果関係の対応から、なんとなく相関分析は相関関係を調べるもので、回帰分析は因果関係を調べるもののような印象を持ってしまうが、
因果関係と相関関係・メモ
「相関関係は因果関係を意味しない」はよく言われることで、これ自体に文句はないのだが、「因果関係とは何か」についてよく考えると、これはまた深い考察が必要である。いずれ独自のページを作って考えたい。
広告
References
|
生存時間解析 について平易に書いた数少ない解説書。 統計のなかでも、生存時間解析はそれだけで 1 冊の本になるほど複雑なわりに、ANOVAや t 検定などと違い使用頻度が低いため、とっつきにくい検定である。 この本では、とくに |
- 重回帰分析について。Link: Last access 2020/06/10.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
