おかしな日本語・疑似相関とは: 定義について考える

UB3/statistics/correlation/correlation_spurious

このページの最終更新日: 2023/02/14


  1. 定義: 相関と疑似相関
  2. 背後因子 (潜在因子) による疑似相関の実例
  3. ちょっとまともな疑似相関

広告

定義: 相関と疑似相関

相関 correlation とは、2 つの量 x と y について「x が増えると y も増える (正の相関)」または「x が増えると y が減る (負の相関)」という関係のことである。例えば、正の相関を散布図にすると以下のようになる。

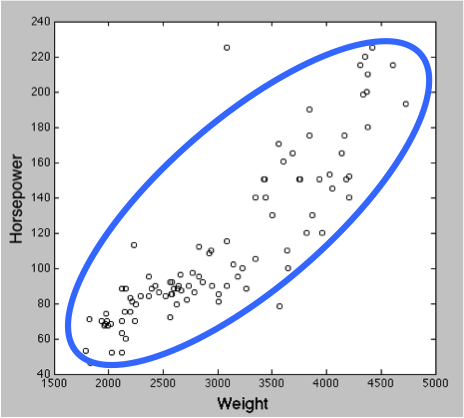
このサイトには、相関に関するページがいくつかある。興味のある人は以下のページを参照のこと。


一方、世の中には 疑似相関 (擬似相関) という言葉もあるが、私はこの言葉を聞くたびに怒りを覚える。このページは、疑似相関という言葉に不満をたれるためのページである。

まず、「疑似」と「擬似」が両方使われているので、これらの定義を調べてみた。

  1. 擬似「本物の見かけを持っている、似せている、似ていて紛らわしい (疑似に通じる)」(Ref)。
  2. 疑似「まぎらわしくて見分けにくいこと」、擬似「何の罪にあたるかを評議する」 (大漢和辞典・大衆館書店による。Ref)。

要するに同じような意味であるが、2 番の大漢和辞典・大衆館書店では言葉の本来の意味にまで言及しており、「日本語で、「手へん」のない「疑似」と同じ意味を表す「擬似」は、中国語から受け継いだことばではなく、日本人が独自に作り出したことばではないか、と思われます。」と書かれている。よって、このサイトでは「疑似」を使うようにしたい。

さて、問題の「疑似相関」の定義である。

  • 二つの事象に因果関係がないにもかかわらず、あるように見えること。相関関係が見出される二つの事象A、Bについて、AとBが共に別の要因によって生起している場合、AとBの間に疑似相関があるという。偽相関。 (goo 国語辞典)
  • 2つの事象に因果関係がないのに、見えない要因 (潜伏変数) によって因果関係があるかのように推測されること。(Wikipedia)

いや、てめーそれ疑似因果だろ。「相関関係が見出される二つの事象A、Bについて」で相関関係は確かにあるのだから、「疑似相関」はおかしいよ。

「疑似体験」では体験が本物ではなく、「疑似科学」は科学っぽく見せているが、科学ではないもののことだ。しかし、この場合は「因果関係」がないだけで「相関関係」はあるのに、なぜ「疑似相関」なのか。

相関と因果はそもそも全く別のことなのに、因果がないだけで、なぜ相関まで否定されるような言い方をされなければならないのか。

ネットで調べてみても、あまりこの意見がないのは非常におかしいと思う。これはつまり相関と因果の違いがはっきり認識されていないということであり、多くのネット記事がこの学問的な違いを意識しない程度のレベルで書かれているということだろう。

英語版 Wikipedia を見てみても、spurious relationship or spurious correlation という項目の説明で、同じような解説が載っている。この誤解は国際的なようである。


広告

背後因子 (潜在因子) による疑似相関の実例

この 統計的消去で擬似相関を見抜こう！ に載っている例について考えてみる。これもやはり相関と因果の混同であり、これらを正しく認識した場合には 交絡 confounding の概念に含まれる考えである。

背後因子を想定した疑似相関の定義は、以下のような形で書かれる。

  • Factor 1 と Factor 2 に相関がみられるが、実はこれらと相関する背後の要因 Factor 3 があり、この影響を取り除くと、1 と 2 の相関はなくなる。この場合、1 と 2 の相関が疑似相関である。

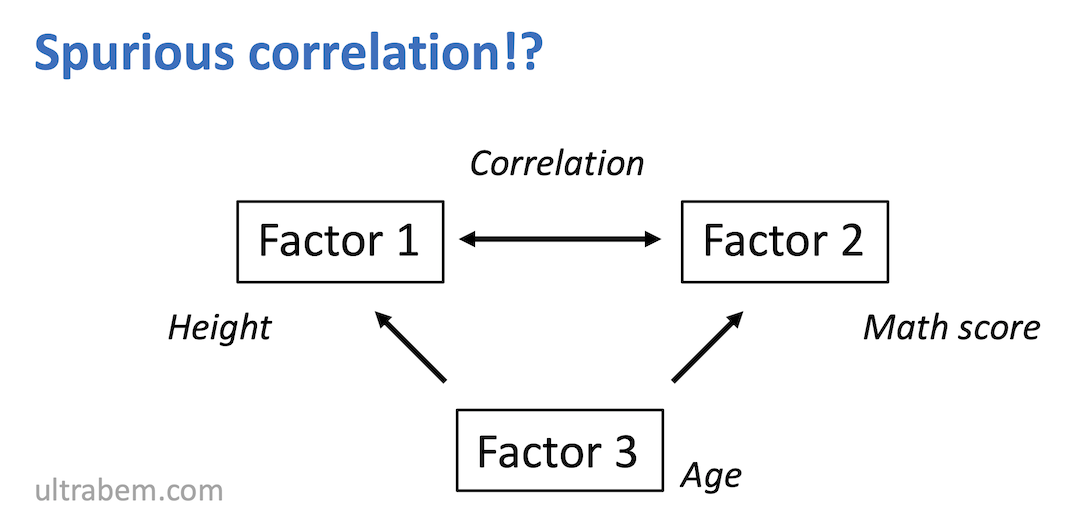
例のページでは、小学生で「身長が高いと算数の能力が高い」という相関のデータをまず示し、「身長が算数の能力に関係しているなんて、すごい発見です！」として、そこから「年齢」の要因を統計的消去で取り除くと、相関がなくなることを示している。

そして、身長と算数の能力は、年齢が背後因子にある「疑似相関」であったと結論。

しかし、このサイトでは「身長」から「算数能力」に一方向矢印を引っ張って「すごい発見です！」と言っていることからも分かる通り、相関であるのに勝手に因果を導入して、統計的消去でそれを自ら否定しているに過ぎない。

身長および算数能力は、年齢に伴って変化する確率変数であり、ここから年齢の影響を取り除いたら、それはもはや身長および算数能力ではなくなる。



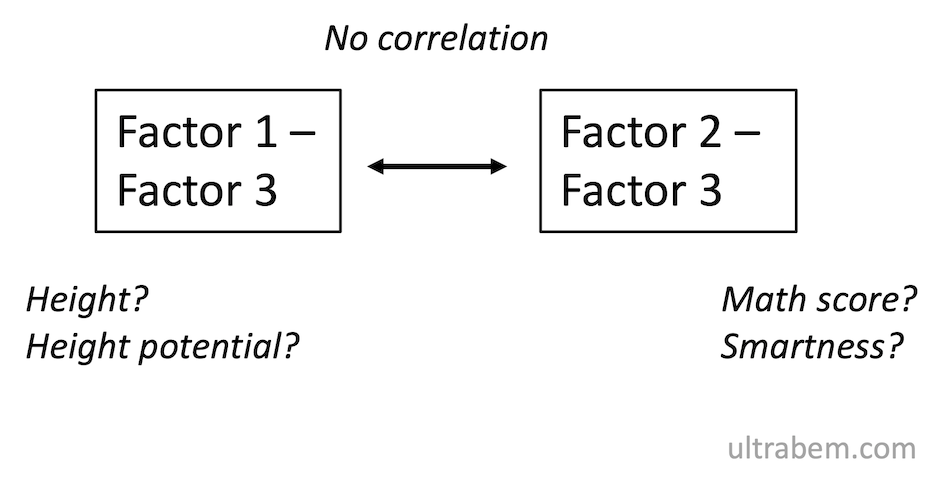
年齢の影響を取り除いて残るのは、「身長ポテンシャル」「生まれ持った算数的かしこさ」のような能力であろう。これらに相関がないのはそりゃそうだが、身長と算数能力には確かに相関があり、その関係は「疑似」でも何でもないのだ。

このデータから、「身長を伸ばせば算数のスコアも上がる」としてしまうのが間違いであり、これはまさに「疑似因果」と呼ばれるべき考えである。

ちょっとまともな疑似相関

サンプリング揺らぎによる相関

ネットで見つけた、唯一「これなら疑似相関と言ってもいいかな」と思える定義。

この togetter には、ノイズもあるがまともな言説がある。「標本集団では相関がみられるが、これはサンプリングの揺らぎに由来するものであり、母集団では相関がみられない状態」なら、疑似相関という言葉を使うことに依存はない。


広告

References

  1. 統計解析 Q & A -相関と回帰分析- Link: Last access 2020/05/11.
  2. Shannon lab 統計データ処理/分析. Link.
  3. 臨床統計 まるごと図解.

生存時間解析 について平易に書いた数少ない解説書。

統計のなかでも、生存時間解析はそれだけで 1 冊の本になるほど複雑なわりに、ANOVAや t 検定などと違い使用頻度が低いため、とっつきにくい検定である。

この本では、とくに Kalpan-Meier 生存曲線、Log-rank 検定、Cox 比例ハザードモデルを重点的に解説しているが、prospective study と retrospective study, 選択バイアス、プラセボなど、臨床統計実験で重要な概念についても詳しい説明がある。臨床でない、基礎生物学の実験ではあまり意識しない重要な点であるので押さえておきたい。

  1. 重回帰分析について。Link: Last access 2020/06/10.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。


↑