1. 主成分分析の概念: 変数を減らす
2. 2 次元から 1 次元に減らす例
3. 寄与率
4. 主成分分析を論文に載せる際の注意点
   • スコアプロット
   • ローディングプロット

関連ページ

• R: mtcars データセットを使った主成分分析

主成分分析の概念: 変数を減らす

主成分分析 (principal component analysis; PCA) とは、データに含まれる変数とは異なる指標を設定し、変数間の関係を把握しやすくするための統計手法である。関連する手法に 主座標分析 PCoA がある。

身体検査の例 (1) がわかりやすかったので、これを例に説明する。

身長と体重がデータとしてあるとき、おそらく両者は図のように正の相関 correlation を示すだろう。

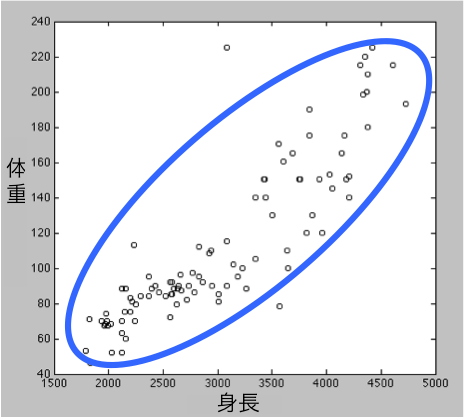
この例のようにデータが 2 つだけならわかりやすいのだが、以下のように多くのデータがあるとどうだろう？

• 身長
• 体重
• 顔の大きさ
• 手の大きさ
• 足の長さ

5 つの数字があるので、これは「5 次元データ」である。これらの数値間の関係を一つづつ検証していくのは複雑で手間がかかる。

しかし、これらのデータに、「体の大きさ」という 新たな指標を導入すると、変数間の関係や特徴を把握しやすくなる。

つまり、データの解釈が「身長と体重が相関する」「身長と足の長さが相関する」などから「でかい人は身長も体重も大きく、足も長い」に変わるのである。

これが主成分分析の基本的な考え方で、この例では「体の大きさ」が 第一主成分 (PC1) と呼ばれる (1)。

もともと身長・体重など複数の指標で表されていたデータを「体の大きさ」という指標で代表させるため、主成分分析によって 5 次元のデータを 1 次元のデータに変換したと考えることができる。ただし、これに伴って情報は損失している。

文献 1 では「肥満の程度」というもう一つの新たな指標 (第二主成分)を考えている。この場合はもとの変数が 5 つ、主成分分析によって生じた新たな指標が 1 or 2 個だが、多くの場合もとの変数はもっと多く、それを 2 つの新しい指標で代表させることが多い。

2 次元から 1 次元に減らす例

主成分分析の「変数を減らす」という概念をもう少し具体的に見てみよう。単純な例として、変数を 2 つから 1 つに減らす場合を考えてみる。

x, y という 2 つの次元をもつデータがあるとする。この場合、まず散布図を作って両者の関係を把握するのがデータ分析の基本である (参考: R の plot 関数、R の ggplot 関数)。

さらに、x と y の回帰直線を引く。回帰分析については、相関分析と回帰分析 およびそこからのリンクを参照のこと。

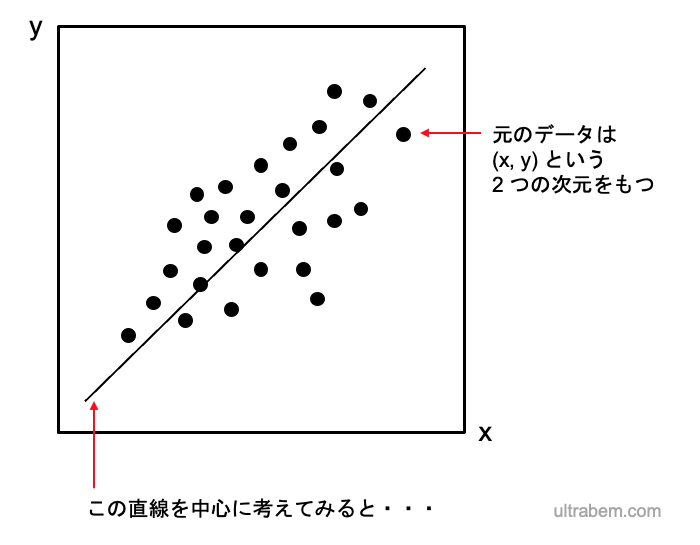
主成分分析では、この x と y の回帰直線を中心にデータを再解釈することになる。わかりやすくするために、図の全体を回転させる。

さらに、全てのデータをこの直線上に下ろしてくる。

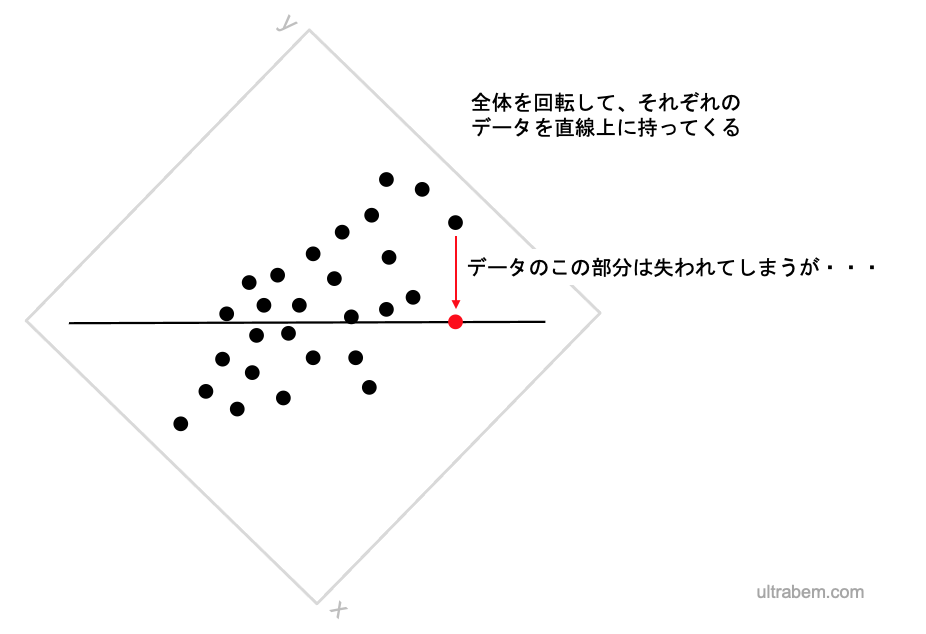
データに含まれる情報の一部は失われてしまうが、全てのデータを直線上に下ろすと、このようにデータ分布を 1 つの値だけで解釈できるようになった。これが新しい変数、PC1 である。

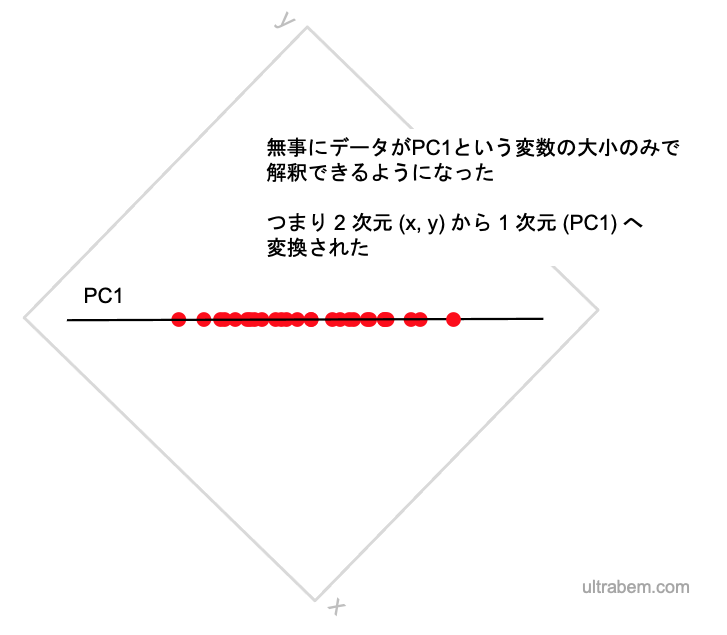
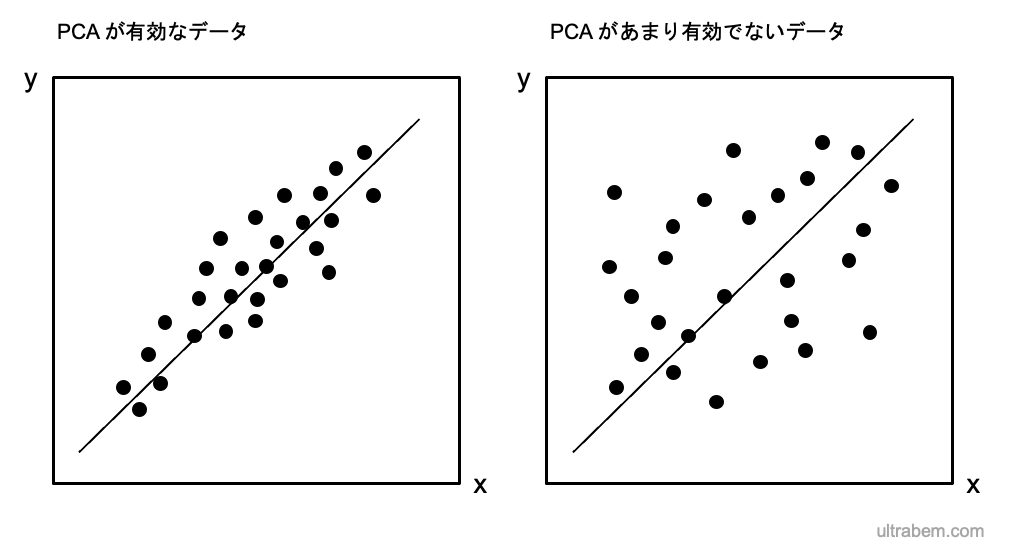
こう考えると、PCA が有効なデータと、あまり有効でないデータがあることがわかる。

左のような、データが回帰直線に近い分布を示しているとき、以上の作業で失われるデータ量は少ない。したがって、PC1 による近似が実際のデータをよく反映する。

一方で、右のようなデータでは失われる情報量が多くなってしまう。

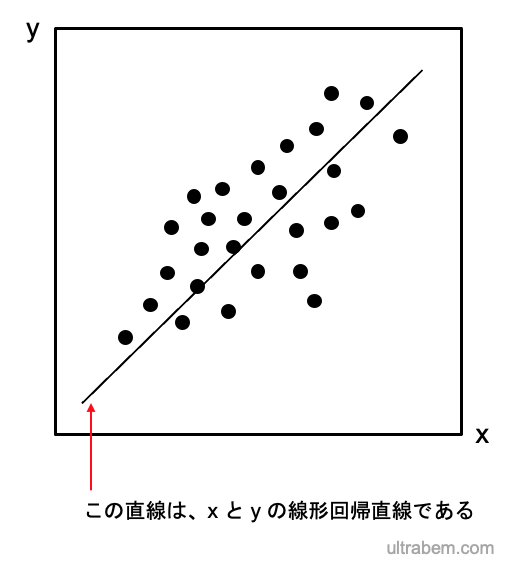
ここで最初の図に戻ってみると、そもそもこの直線は、x と y の線形回帰であり、y = ax + b で表される。これが、テキストに書かれている「主成分は、各変数の線形結合として与えられる (1)」の意味である。

寄与率

新たに作られた主成分 (新しい指標) は、もとのデータをある程度表現しているはずである。この程度を表すものが 寄与率 contribution rate である。

一般に、累積寄与率が 80% を超えたら、以後の主成分は無視するのが普通である (3)。もちろんデータに応じて異なるが、80% が一つの目安のようだ。

主成分分析を論文に載せる際の注意点

一般には、スコアプロットとローディングプロットの両方を載せる必要がある。

スコアプロット

文献 2。

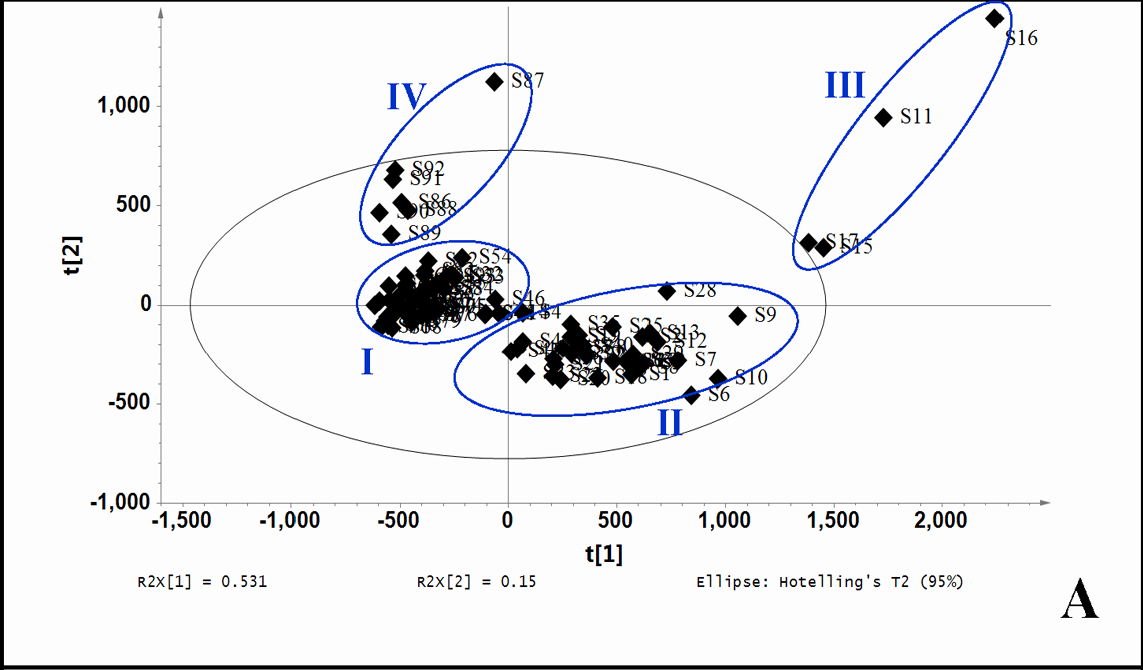
Nam et al., Metabolites 10, 376, 2020 Fig. 2C。

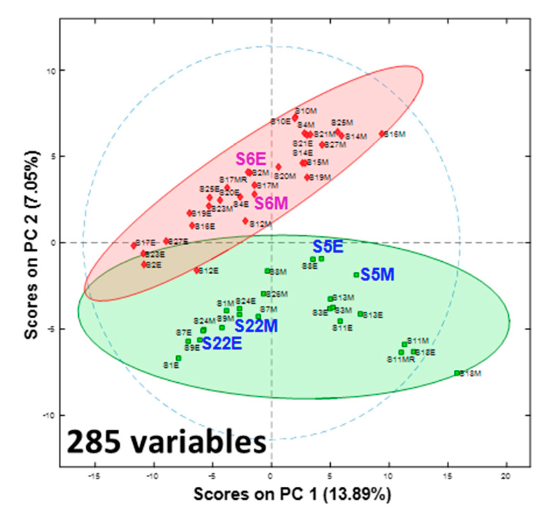
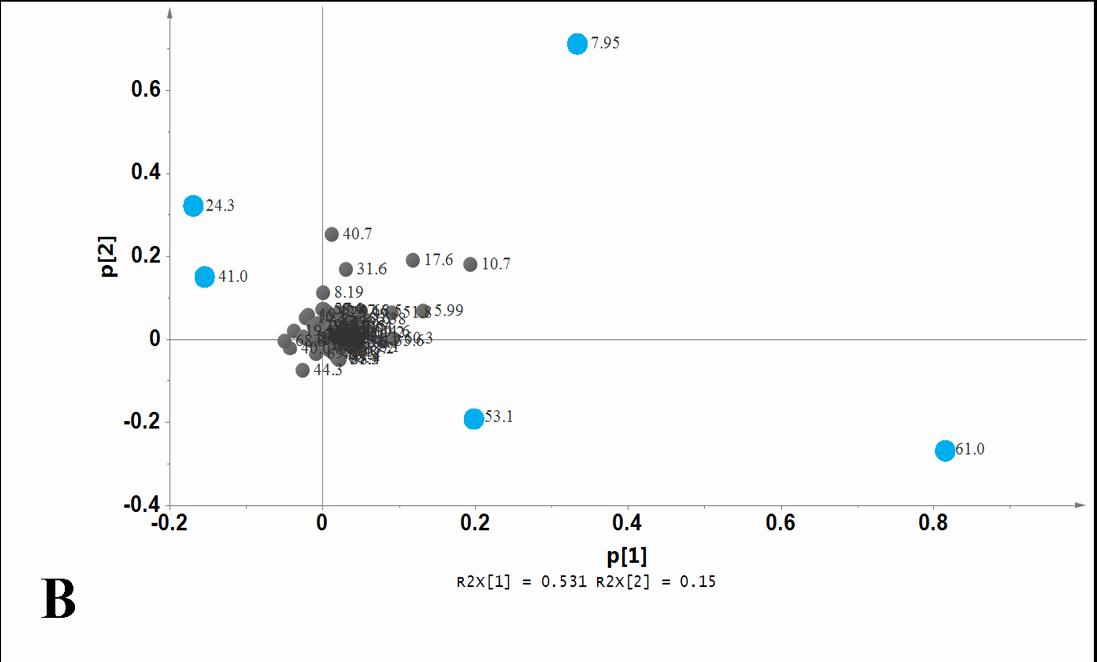
ローディングプロット

主成分スコアと元の変数との相関係数を因子負荷量、因子負荷量の散布図をローディングプロットと呼ぶ (参考)。

この図も文献 2 から。

References

1. 加納 2002a. 主成分分析 初心者向けテキスト. Pdf file.
2. Yao et al., 2015a. Discriminatory Components retracing strategy for monitoring the preparation procedure of Chinese patent medicines by fingerprint and chemometric analysis. PLoS ONE 10, e0121366.
3. 主成分分析 (暗号化されていないページのため、リンクを張っていません). http://www.snap-tck.com/room04/c01/stat/stat16/stat1601.html Last access 2023/01/01.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。

↑