ばらつきの指標: 範囲、分位数、分散、変動係数など
UB3/statistics/basics/spread
このページの最終更新日: 2025/11/23- 概要: ばらつきの指標
- 範囲
- 分位数
- 分散と標準偏差
- 変動係数
広告
概要: ばらつきの指標
このページの解説の多くは、Fundamentals of Biostatistics に基づくものである。
平均値のページ にまとめたように、算術平均、幾何平均、中央値、最頻値などは集団の特性を表す値である。これらに加えて、
範囲 Range
シンプルに最大値から最小値を引くと範囲 range を求められる。範囲が大きいとばらつきは大きい。直感的にわかりやすく、計算しやすいことがメリットであるが、外れ値に非常に大きな影響を受ける (1)。
分位数 Quantile
分位数 quantile とは、中央値 median に近い概念である。データを大きい順または小さい順に並べて、数えていくという手法をとる。
パーセンタイル値
パーセントを用いるパーセンタイル値 percentile は、よく使われる分位数の一つである。データを小さい順に並べて、小さい方から数えて p% になる値が pth percentile である。厳密に定義すると、次のようになる (1)。
- The (k+1)th largest sample point if np/100 is not an integer (where k is the largest integer less than np/100).
- The average of the (np/100)th and (np/100 + 1)th largest observations if np/100 is an integer.
10th と 90th パーセンタイルは、ばらつきの指標としてよく使われる値である。
広告
分散と標準偏差
パーセンタイルが中央値に近い概念であるのに対して、分散および標準偏差は算術平均に近い概念である。したがって、分布が図 (Public domain) のような 正規分布 に近い場合に、分散と標準偏差はより意味のある値になる。
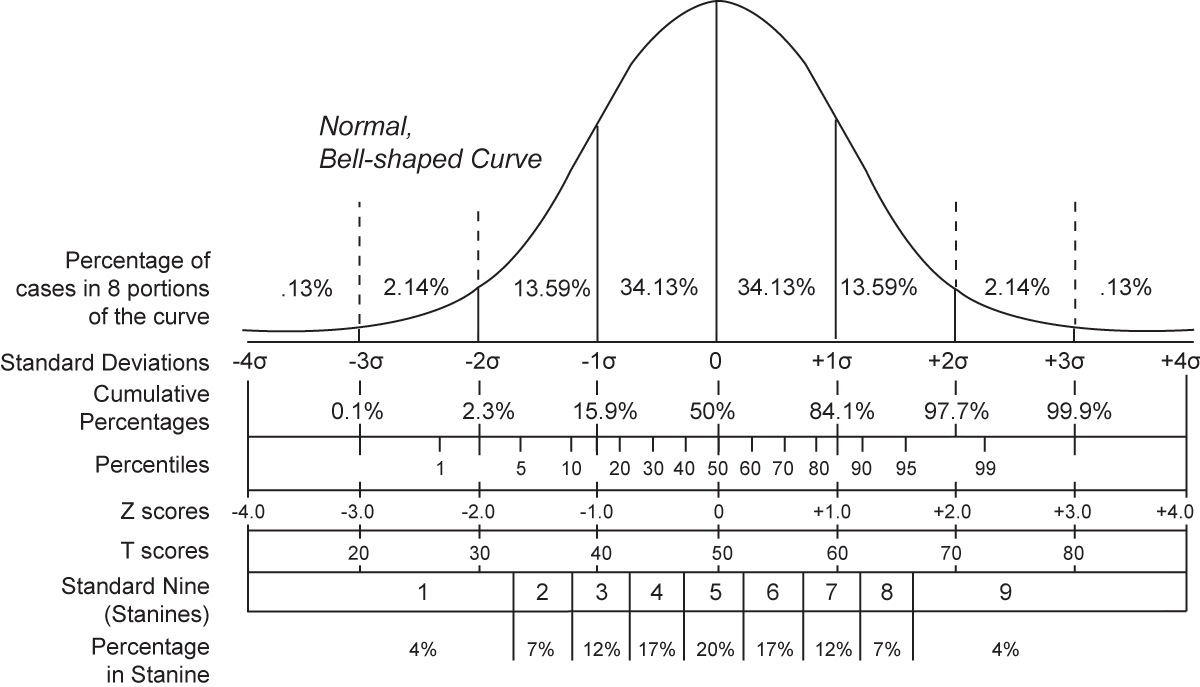
詳細は 分散のページ および 標準偏差と標準誤差のページ にまとめた。
変動係数 Coefficient of variation
変動係数 Coefficient of variation (CV) は、次の式で定義される (1)。
CV = 標準偏差 σ/算術平均
パーセントで表されることもある。データの値が大きい (つまり平均値が大きい) と、それに伴って標準偏差の数値も大きくなる。平均値が著しく異なる集団のばらつきを比べるとき、標準偏差をそのまま比較するのはフェアではない。
変動係数は、そのような場合に有効である。平均値で標準偏差を割ることで、「平均値がでかい」という影響を打ち消し、ばらつきを比べられるようにしている。
広告
References
Rosner 2016a. Fundamentals of Biostatistics.
|
平均値や中央値から始まり、t 検定、ANOVA、回帰分析まで、普通の論文で使う統計手法を網羅している本。とにかくグラフ付きの実例が多く、さらにその実例は論文からとられているので、実践的な生物統計を学びたい人にはおすすめの一冊。 統計の本はとっつきにくいものが多いが、2016 年と比較的最近の本であることも特徴だ。著者はハーバード公衆衛生の Bernard Rosner。経歴を見ると医学統計のエキスパートだが、この本は たぶん高校の上級から大学の学部生あたりが基本的なターゲットで、研究に使う際に統計の基礎をチェックしたい研究者にも適した本になっている。 |
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
