尺度水準の定義と実例: 名義、順序、間隔、比例

UB3/statistics/basics/scale

このページの最終更新日: 2024/09/30

  1. 概要: 尺度水準とは
  2. 名義尺度
    • 名義尺度での炎上例
  3. 順序尺度
    • リッカート尺度 Likert scale
  4. 間隔尺度
  5. 比例尺度

広告

概要: 尺度水準とは

それぞれの尺度水準の特徴を簡単にまとめた (2)。

Fundamentals of Biostatistics, 8th edition では、間隔尺度と比例尺度を合わせて cardinal data と呼んでいる。Cardial data のうち、0 が適当にとられているものが interval scale、0 が固定されているものが ratio scale という説明だ。Cardial data に対応する日本語が何なのか、ちょっとわからない。

カテゴリー変数 categorical variable とは、男女、血液型のようなカテゴリーの変数である。名義尺度および順序尺度になることができる (参考)。


水準 簡単な説明と例 最頻値 中央値 相加平均 相乗平均 分散

名義尺度
Nominal scale

単なるカテゴリー

例: 電話番号
OK
-
-
-
-

順序尺度
Ordinal scale

順番のみに意味、演算不可

例: 徒競走の順位
OK
OK
-
-
OK

間隔尺度
Interval scale

差に意味があり、比にはない

カレンダーの日付、摂氏温度
OK
OK
OK
-
OK

比例尺度
Ratio scale

ゼロが存在、比に意味あり

長さ、重さ、絶対温度
OK
OK
OK
OK
OK

名義尺度

名義尺度 nominal scale とは、データを単にカテゴリーに分けた変数 である。以下のようなものが名義尺度に相当する。これらのデータは、度数、最頻値 には意味があるが、平均 mean、分散 variance などには意味がない。

  • 電話番号
  • 遺伝子の ID
  • 紅白、A, B, C... などのグループ分けも、それぞれ数字に対応させることができるので、本質的に名義尺度と同じである。

名義尺度で炎上

2016 年 1 月に、京大が以下のようなプレスリリースを出した。問題になったので、現在は削除されているようだ。

ビッグデータの解析で薬の副作用予測がほぼ100％可能に

江谷典子 医学研究科特定研究員は、薬剤やその副作用、疾患の原因となる遺伝子などのビッグデータを解析することで、副作用をほぼ確実に予測できるとの研究成果を発表しました。加えて、既存の薬剤の中で、元々のターゲット以外の疾患に効果を発揮する可能性があるものについての予測も行い、いままで治療薬が公開されていない疾患に対して300件以上の候補を発見しました。

本研究成果は8月7日、Springer 社の学術雑誌 Journal of Big data に掲載されました。


削除したものを曝しておくのも可哀想な気がするが、100%予測可能という誇大広告の罪は大きいと思う ので、例として使わせてもらう。

この論文では、目的変数 y' について


y' = a1*SCORE + a2*ACT + a3*GeneID + b


という式を立て、y' を薬の副作用のパラメーターとして定義している。ここで不思議なのが、名義変数である GeneID が線形結合の中に登場する ことである。これは、例えて言えば「ある人の体重 (kg) = a1*身長 + a2*胸囲 + a3*腹囲 + a4*アイウエオ順の出席番号」のような感覚である。変数の性質をよく理解していないと、このようなミスを犯すことになるので気をつけたい。

既存のパラメーターに対してオーバーフィッティングを行なった結果、100% フィットということになった。これは、今後の副作用を予想できることとは別の話である。このあたりも、いずれ回帰分析のページでまとめたい。

順序尺度

順序尺度 ordinal scale で記述されるデータでは 数字の順番に意味があるが、数字に対して演算を行うことはできない。例えば、以下のようなデータである。

  • 徒競走の順位: 1 位は 2 位よりも上位であるが、何かの値が 2 倍であることを意味するわけではない。
  • 原発事故のレベル

度数、最頻値に加えて、中央値 を意味のあるデータとして扱うことができる。順序尺度のデータは、順序カテゴリーデータとも呼ばれる。


リッカート尺度

アンケートでよく使われる「文の内容にどの程度同意できるか」を基準とした尺度をリッカート尺度 Likert scale という。Likert は人名である。例えば、以下は 5 段階のリッカート尺度である。

統計学は難しいと思う。

  1. 非常にそう思う
  2. そう思う
  3. どちらとも言えない
  4. あまりそう思わない
  5. 全くそう思わない

質問の内容や選択肢からわかるとおり、数字の順番に意味はあるが、例えば「1. 非常にそう思う」は「2. そう思う」の何倍であるかという議論はできない。したがって、リッカート尺度は原則的には順序尺度に相当する。

ただし、複数の項目の回答を累積する場合は間隔尺度として扱うらしい。この場合、分布が正規分布に従うという条件付きで、パラメトリックな検定を適用できる。

英語の例も載せておこう (4)。Strongly agree などといった言葉が使われる。


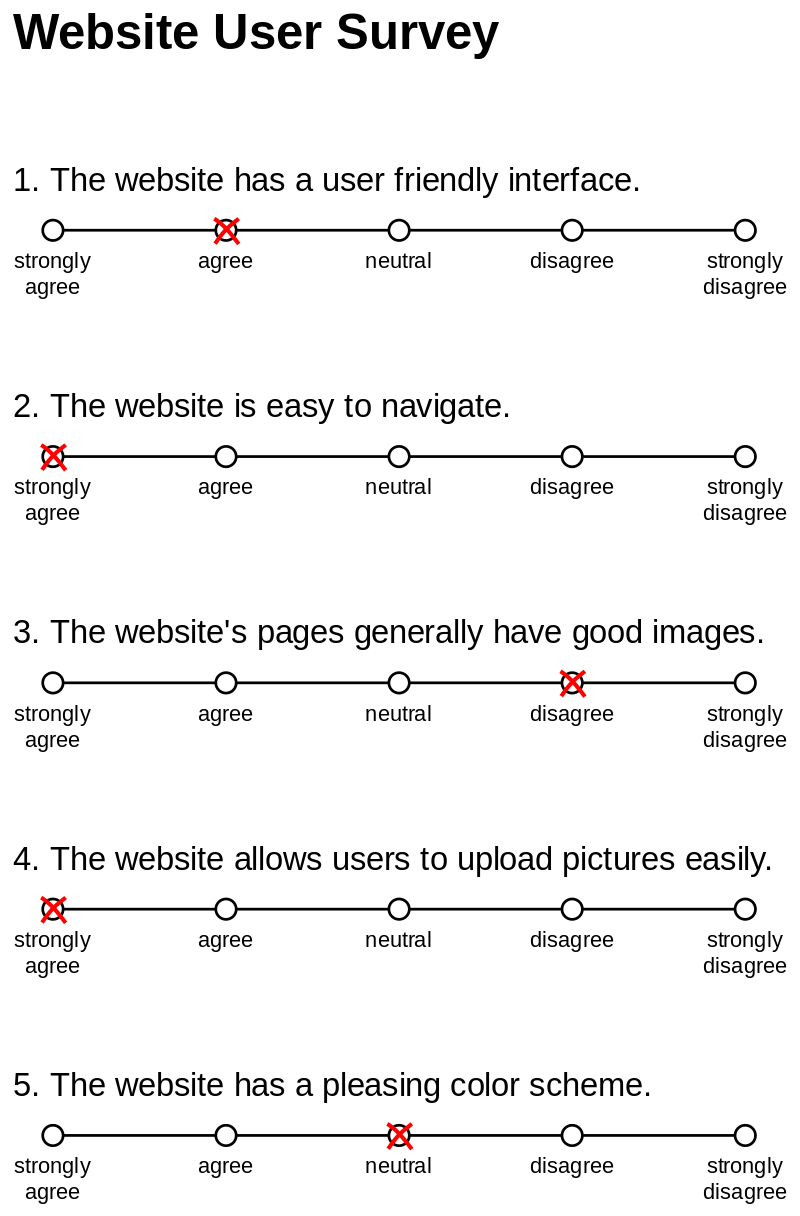
リッカート尺度
広告

間隔尺度

間隔尺度 interval scale で記述されたデータでは、目盛りが等間隔になっており、数値間の差に意味が あるが、比には意味がない。

  • カレンダーの日付: 1/1 と 1/3 の間には 1 日の時間がある。これは 1/5 から 1/9 日の間の 3 日間の 3 分の 1 であると言える。しかし、それぞれの日付の比をとった 3 と 1.8 という数値を比較する意味はない。
  • 摂氏温度、華氏温度

最頻値、中央値に加え 相加平均 (算術平均) を代表値として使うことができる。

比例尺度

間隔尺度の基準を満たし、さらに ゼロを原点として考えられるもの を比例尺度 ratio scale という。比率尺度とも呼ばれる。

  • 長さ、重さなどの物理量: 原点としての 0 が存在する。摂氏 0 度の 0 は便宜上の値であり、長さの 0 とは意味が異なる。
  • 絶対温度

広告

References

  1. 統計データの種類、尺度水準. Link.
  2. 尺度水準. Link.
  3. Rosner 2016a. Fundamentals of Biostatistics.

平均値や中央値から始まり、t 検定、ANOVA、回帰分析まで、普通の論文で使う統計手法を網羅している本。とにかくグラフ付きの実例が多く、さらにその実例は論文からとられているので、実践的な生物統計を学びたい人にはおすすめの一冊。

統計の本はとっつきにくいものが多いが、2016 年と比較的最近の本であることも特徴だ。著者はハーバード公衆衛生の Bernard Rosner。経歴を見ると医学統計のエキスパートだが、この本は シグマ記号の意味が実例つきで紹介されている ことからも分かる通り、平易な解説になっている。

たぶん高校の上級から大学の学部生あたりが基本的なターゲットで、研究に使う際に統計の基礎をチェックしたい研究者にも適した本になっている。



  1. By <a href="//commons.wikimedia.org/wiki/User:Mr.Olas" title="User:Mr.Olas">Nicholas Smith</a>vectorization: <span class="int-own-work" lang="en">Own work</span> - <span class="int-own-work" lang="en">Own work</span>, based on <a href="//commons.wikimedia.org/wiki/File:Example_Likert_Scale.jpg" title="File:Example Likert Scale.jpg">File:Example Likert Scale.jpg</a>, CC BY-SA 3.0, Link.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。


↑