信頼区間 confidence interval とは: 定義、実例など

UB3/statistics/basics/confidence_interval

このページの最終更新日: 2024/09/30

信頼区間の定義: 「統計学入門」を中心に
- 信頼区間の意味するところ
「確率」という言葉
- ゴミ箱の例え
- 天気予報の話
- 黒木玄氏のコメント
R で信頼区間を算出する

信頼区間の定義: 「統計学入門」を中心に

信頼区間 confidence interval は、統計学では最初の方に習う項目であるが、意外と難しい概念である。ネットにもいろいろと適当な情報があるが、ここはまず教科書から定義を拾ってみよう。

統計学入門 (Amazon link) では、「区間推定」の項目 (11.5) で関連する概念を

区間推定とは真の母数θが、ある区間 (L, U) に入る確率を 1 - α (α はθが区間に入らない確率) 以上になるように保証する方法であり、

P(L≤θ≤U) ≥ 1 - α

となる確率変数 L、U を求めるものである。

のように説明しており、続いて定義が以下のように示されている。

L: 下側信頼限界 lower confidence limit
U: 上側信頼限界 upper confidence limit
1 - α: 信頼係数 confidence coefficient
区間[L, U]: 100(1 - α)% 信頼区間 confidence interval

母数θは、母集団を代表するパラメーターの一般的な表現であり、多くの場合は母平均だと思って良い。対応する標本集団のパラメーターは、θの上にハットをつけて表現する。

以上が信頼区間の「ちゃんとした」定義であるが、この説明が難しいと感じる場合は、以下のページをお勧めする。

生物学実験における統計: 母集団などの解説

信頼区間の意味

「統計学入門」の解説は、以下のように続く (下線引用者)。

なお、同ーの母集団から抽出した標本でも、標本ごとに信頼区間の推定値は変化する．θは未知ではあるが決まった定数である．したがって、一つの標本から信頼区間を具体的な数値として推定してやれば、これは信頼区間に含まれるか含まれないかのいずれかしかない．すなわち、具体的に数値として計算した現実の信頼区間に対して、“1 - α の確率でθを含む” ということはない．信頼区間の意味は、繰返し多くの異なった標本について信頼区間をここで述べた方法によって何回も計算した場合、θを区間内に含むものの割合が 1 - α となるということである.

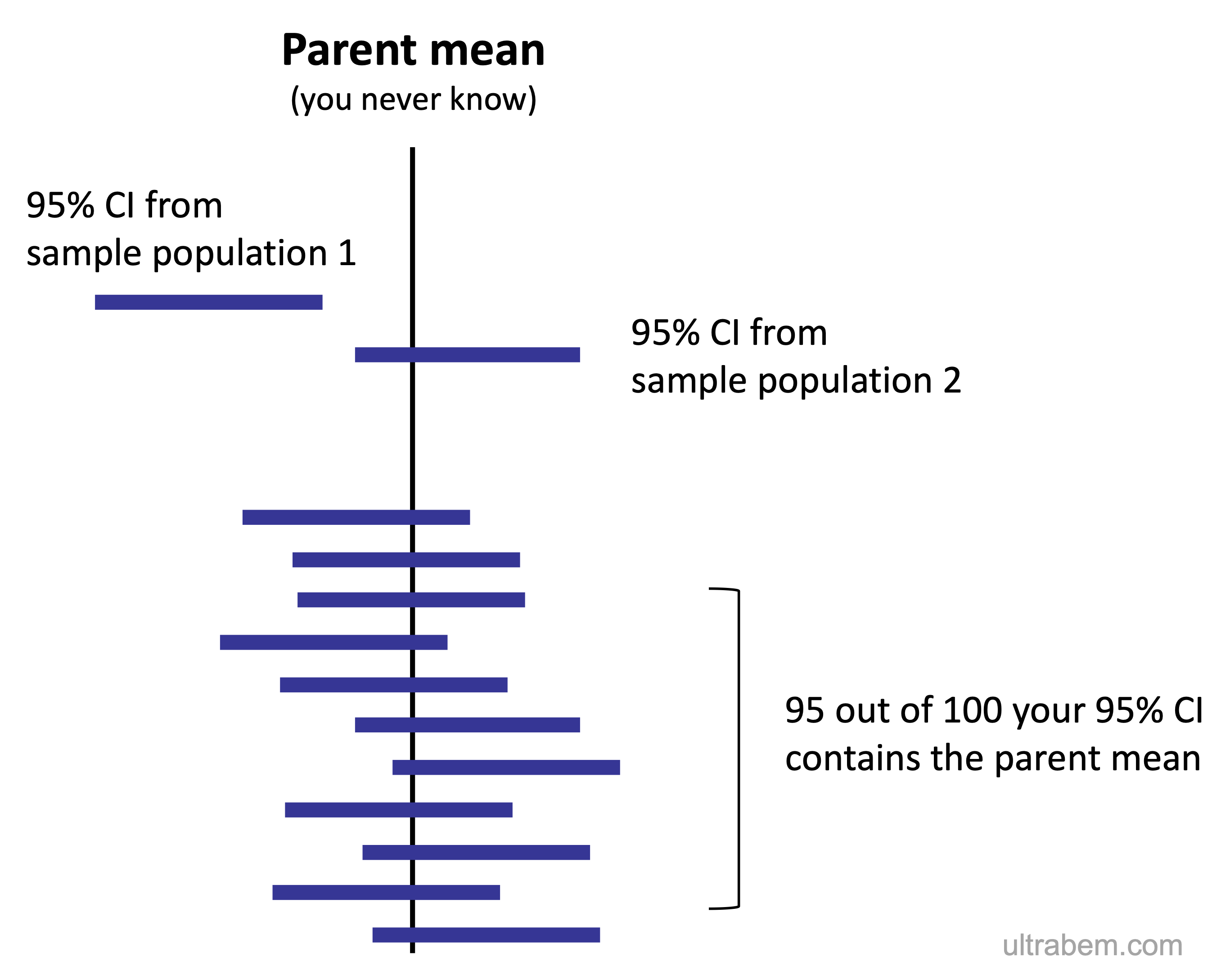
推定値を母集団の平均 parent mean として図示すると以下のようになる。ポイントは、

通常は母集団のパラメーターは未知なので、母平均もわからない。しかし、数値がわからないだけで、母平均は一つの値として存在する。
標本集団をとってきて、95% CI を計算する。95% CI は一定の区間として与えられる。
この作業を 100 回繰り返したら 100 個の 95% CI が得られるが、そのうち 95 個は母平均を含む範囲である。

「確率」という言葉

上の図、または統計学入門の記述のように、信頼区間の意味は、繰返し多くの異なった標本について信頼区間をここで述べた方法によって何回も計算した場合、θを区間内に含むものの割合が 1 - α となるということであると覚えておけばとりあえずは安全であるので、これをお勧めする。

ここからは私個人の考えで、教科書では否定されているものの、これは「1 - α の確率で θ を含む」と言って良いのではないかと考えてみる。

「統計学入門」では次のように書かれている。

一つの標本から信頼区間を具体的な数値として推定してやれば、これは信頼区間に含まれるか含まれないかのいずれかしかない．すなわち、具体的に数値として計算した現実の信頼区間に対して、“1 - α の確率でθを含む” ということはない．

ネットでもこれに準じた記述をよく見る。曰く、

「95%信頼区間」とは、母平均が95%の確率でその範囲にあるということを表しています。これは、「正規分布に従う母集団から標本を取ってきてその平均から95%信頼区間を求めた時に、その区間の中に95%の確率で母平均が含まれる」という意味だと思う人がいるかもしれませんが、これは間違いです (2)。
正しくは、「母集団から標本を取ってきて、その平均から95%信頼区間を求める、という作業を100回やったときに、95回はその区間の中に母平均が含まれる」という意味です (2)。

とあり、その根拠として母平均が動かないために「確率」という言葉が使えないとしている。ここが納得いかないポイントである。母平均は動かないが、信頼区間は動くのだ。つまりサンプリング毎に異なる 95% CI が出てくる。なぜ、母集団が動く場合には確率という言葉が使えるのに、信頼区間が動く場合には使えないのか。

文献 3 ではもう少し踏み込んでいるが、要は同じことを言っている。1、2 のどちらが正しいか？という問いかけがあり、

その 95% 信頼区間の中に、95% の確率で真値が入る。
真値は固定されており、仮に100回試験をした場合、100回中5回くらいは真値を含まないことがある。

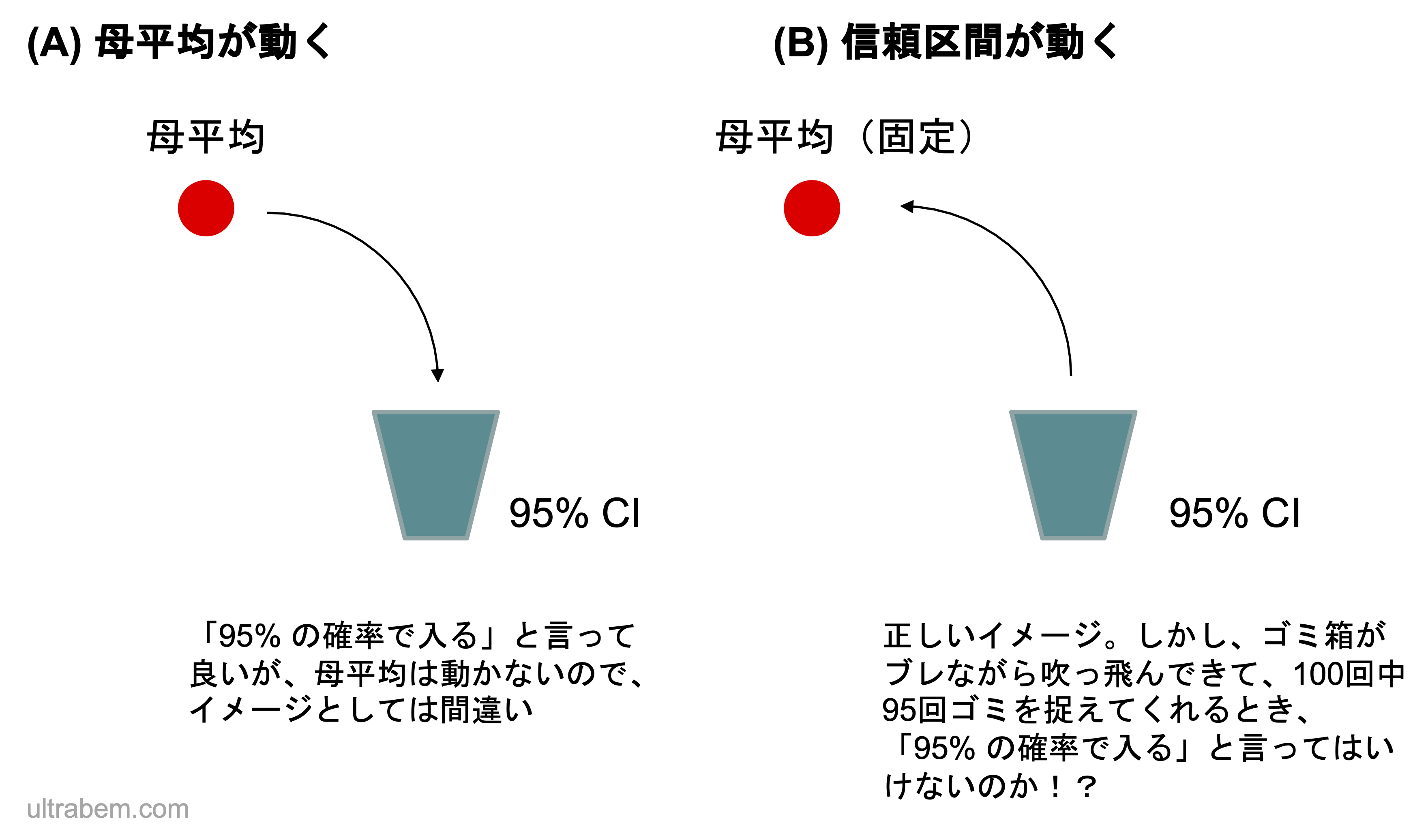
(中略)

1 の場合ですと、95% 信頼区間が固定されており、真値が動いているイメージです。

違います。

真値が固定されていて、95%信頼区間がデータによって変わりうるのです。

という解説があるのだが、選択肢にない「イメージ」を勝手に出してきて、それに「違います」とかいってダメ出しされても困るのである。

私が「母平均は、95% の確率で 95% CI に含まれる」と「95% CI を 100 回算出したら、そのうち 95 個が母平均を含む」が同じであると考える理由をまとめてみる。

ゴミ箱のイメージ

「母平均は定数で確率変数ではないので、これに対して確率という言葉は使えない」というのが、「母平均は、95% の確率で 95% CI に含まれる」と言ってはいけない根拠とされている。

しかし、ここでいう「95% の確率」は含まれるという事象に対しての言及であり、「固定された母平均」vs「無作為抽出で得た 95% CI のゆらぎ」を確率で語るのは全く問題ないはずである。下の項目にまとめているが、数学者の黒木玄氏も同じ見解を繰り返し表明している。

降水確率

この理屈が通るなら、「降水確率 50%」という言葉もダメなんじゃないかという話。

雨は「降る」か「降らない」かのいずれかしかない。すなわち、具体的に今日の天気を予想するとき、現実の天気に対して「** の確率で雨が降る」ということはない、ということにならないだろうか？

気象庁のページには、「降水確率30％とは、30％という予報が100回発表されたとき、その内のおよそ30回は１mm以上の降水があるという意味であり、降水量を予報するものではない。」のように定義されている。

信頼区間の内容に直してみると、「信頼区間95%とは、信頼区間95%の範囲が 100 回計算されたとき、その中の 95% は母平均を含むという意味である」となる。別に何の問題もない気がする。

黒木玄氏のコメント

数学者、黒木氏のコメントでも、このような形で「確率」という言葉を用いることは数学的に完璧に正しいと書かれている。例えば、このページには以下のようにある。

母集団からの無作為抽出に関する統計学では、無作為抽出で得たサンプルの確率的な揺らぎによって生じる統計分析の誤差や誤りを分析することになります。だから、サンプルの確率分布で確率を語ることは統計学の最も基本的な考え方です。続く

また、ツイッターでも「統計学入門」にみられる確率から割合への言い換えには意味がないと明言している。なお、最後のツイートの「添付画像」は、上でも引用した統計学入門の「なお、同ーの母集団から抽出した標本でも・・・」の部分である。

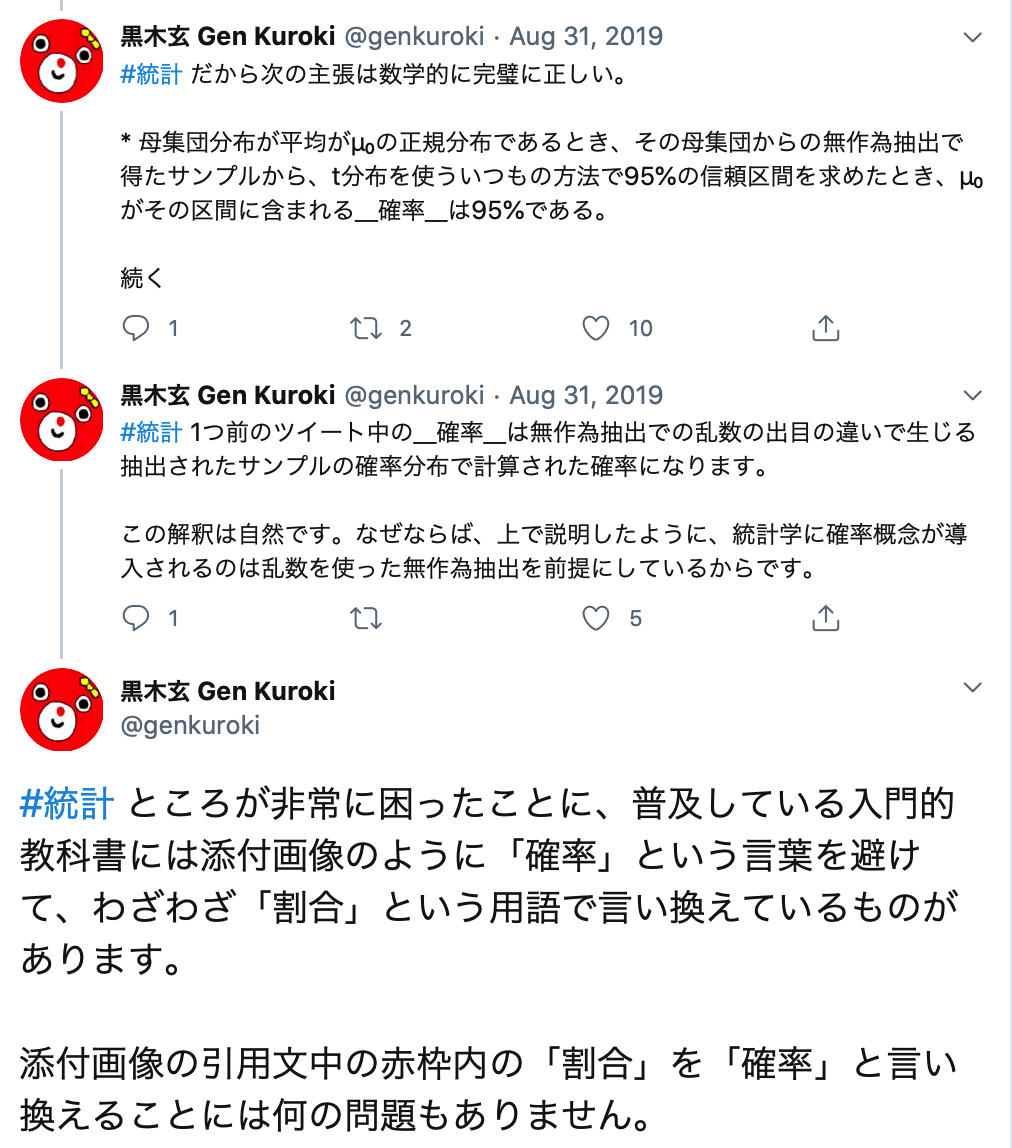
一方で、同氏は「統計学入門」の様々な記述や、上記の信頼区間の説明自体には批判的である。そのポイントは「確率」という言葉の使い方や数学的な厳密さではなく、実際に統計学を使用する際に注意しなければならない点への配慮が足りないという点である。

すなわち、この信頼区間の例について言えば、現実的なデータで 95% 信頼区間を計算し、それを 100 回なり繰り返しても、母集団の分布によって母平均が 95% 信頼区間に含まれる「確率」は異なり、実際には 95% にはならないということのようだ。黒木氏のツイートの言葉を借りれば、「信頼区間の信頼性がその計算に用いた数学的モデルの現実における妥当性に依存」「95%信頼区間はデータだけでは全然決まらず、計算するために使った数学的モデルに大きく依存」する。

実際にデータが正規分布しているかどうかが、信頼区間の信頼性に関わる重要な要素である。ここを強調せずに、安易に正規分布を仮定している教科書は改善が必要、とのこと。

R で信頼区間を算出する

t.test 関数で 95% 信頼区間を計算することができる。詳細は R で信頼区間を計算するのページへ。

References

統計学入門.

確率の基礎、確率分布、仮説検定、回帰などについてわかりやすく解説してある本である。

古い本であるが、レベルを落とさずに、わかりやすくかつバランスよく必要な内容を網羅しており、もっともお勧めの入門書である。これを教科書にして一連の講義を受けることができる学生は幸せである。

付表として正規分布表、t 分布表、F 分布表がついており、これも意外と役に立つ。練習問題とその解答もついている。

95% 信頼区間のもつ意味.Link: Last access 2020/03/15.
95% 信頼区間の求め方とは？いちばんやさしい医療統計. Link: Last access 2020/03/15.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。