1. 概要: 系統樹とは
   • 種系統樹と遺伝子系統樹
   • 無根系統樹と有根系統樹
2. 系統樹の作成方法
   • 距離行列法
   • 節約法
   • 最尤法
   • 系統樹作成の際の一般的注意点
3. 系統樹の評価
   • Bootstrap 法

概要: 系統樹とは

下の図 (Public Domain) のように、生物種や遺伝子間の進化的距離を算出し、それを樹状の図で表したものを 系統樹 phylogenetic tree という。

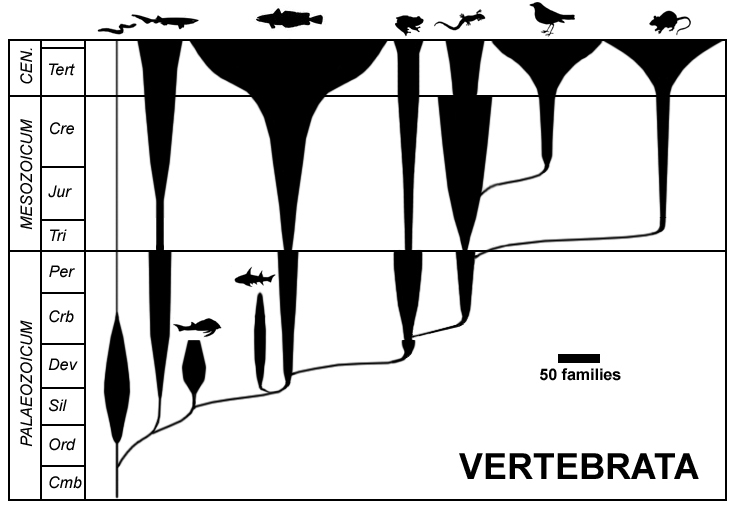
まず、系統樹を理解するために基本的な用語を定義しておく。

種系統樹と遺伝子系統樹

種系統樹は種間の関係を、遺伝子系統樹は遺伝子間の関係を表した系統樹である (3)。両者を区別することが、分子系統樹を理解するための第一歩である。

• 生物種間の関係は、かつては形態 (脊椎がある、羽があるなど) に基づいて推定されていたため、形態に基づいた 種系統樹 species tree が主流であったと思われる。
• 現在よく見られるのは、塩基またはアミノ酸配列の情報を用いて遺伝子間の距離を算出した 遺伝子系統樹 gene tree である。

種・遺伝子系統樹が一致するとは限らない。もっともはっきりした例は、複数の遺伝子ファミリーがある場合である。例えばヘモグロビンとミオグロビンは共通の祖先遺伝子から進化した分子であり、これらの遺伝子の関係は遺伝子系統樹で表される。

一方、種・遺伝子系統樹が一致する場合もある。16S rRNA 配列による遺伝子系統樹は、これが種間の進化関係を表すことを想定して作られたものである。つまり、16S rRNA という遺伝子配列から種の進化を推定しようとしている。

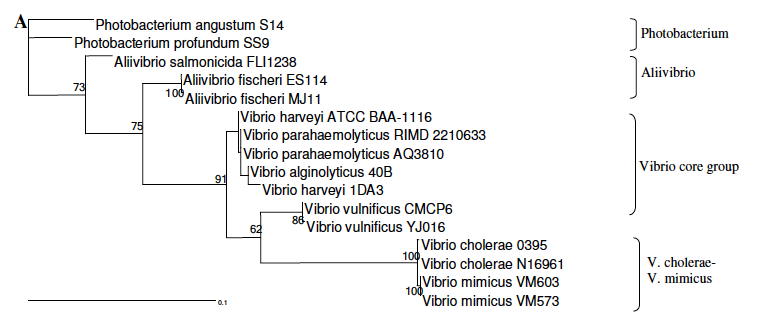
系統樹の例 2: 16S rRNA 配列、最尤法 maximum likelihood method で作成したビブリオ属の分子系統樹 (1)。

無根系統樹と有根系統樹

押さえるべき重要な概念は以下の通りである。

1. それぞれの 遺伝子 (アミノ酸) 配列を結ぶ枝 branch の長さが、遺伝的距離 (配列が異なる度合い) に比例する (2)。
2. ただし、配列から算出されるのは相対距離のみであり、時間的にどの分類群が古いのかという情報は与えられない。
3. 系統樹に含まれる全ての分類群の、最も新しい共通祖先を「根 root」という (図、ref 7)。。Root は、系統樹の中では最も古い生物ということになる。Root を設定すると、この古い祖先からの進化の道筋という形で系統樹を解釈できるようになる。
4. 分岐年代を算出したい場合には、root を設定し、これに化石年代などの情報を含めて推定する。

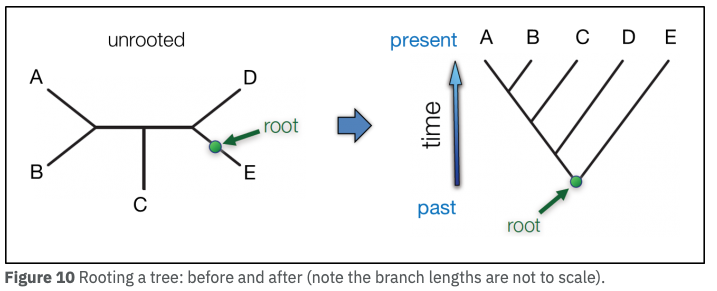
根の選び方には、以下の 2 通りがある (7)。

アウトグループ法 Outgroup rooting:

他のグループから最も離れていることがわかっている配列 (または配列群) をアウトグループとして指定し、そのグループと他の配列の分岐点を root とする。アウトグループは、その他の配列と近い方が望ましい。離れ過ぎていると、変異が saturation している可能性があるため。

ミッドポイント法: Midpoint rooting:

全ての配列が同じ速度で変異していると仮定するため、使用には注意が必要である。2 つの最も長い branch の中央に root を設定する。

系統樹を可視化する TreeView などのソフトでは、根の有無を指定でき、さらに midpoint rooting または outgroup というオプションがある。つまり、どちらの方法も選べるようになっている。

系統樹の作成方法

系統樹を作成するアルゴリズムは複数あるが、大きく以下の 3 つに分類することができる (3)。

1. 距離行列法 distance matrix method
2. 節約法 parsimony method
3. 最尤法 maximum likelihood method

距離行列法

距離法 distance method とも呼ばれる (3)。データセットに含まれる配列の進化的距離を算出し、これに基づいて系統樹を作る。

節約法

進化の過程で生じた置換が最小限であることを仮定し、系統樹を作る (3)。

最尤法

原理については、以下のようなさまざまな表現がある。

• 特定の 1 塩基または 1 残基に着目し、確率計算を行って最も可能性の高い樹形を検索する。これを全ての塩基について繰り返す (3)。
• 尤度が最大になるような系統樹を求める方法 (6)。尤度とは、ある樹形 (仮定) に沿って遺伝子が進化したとき、現在の配列セットが得られる確率である。

どのモデルを選択するかは、ProtTest というソフトウェアを使うと良さそうである。

• ベイズ法は、ベイズの事後確率 Bayesian posterior probability を最大にするような系統樹を作る方法である。
• 事後確率は、事前確率および尤度の積として求められる。事前確率は不明なので、これを MCMC で推定することになる。
• モンテカルロ法は、ランダムな試行を繰り返して目的の値を近似的に求める方法である。ブートストラップ法 もこれにあたる。
• 通常のモンテカルロ法では、試行がそれぞれ独立であるが、マルコフ連鎖モンテカルロ MCMC では、前の試行の結果に影響されるという立場をとる。
• Metropolis-Hastings のアルゴリズムというものを使うと、事後確率の推定をすることができるらしい。ある試行の結果から、次の試行の結果を確率的に推定するということ。
• ベイズ法では、最初はランダムな系統樹からスタートし、一部が異なる次の世代の系統樹を得る。これを採用するか棄却するかを判定し、系統樹が定常状態になるまで繰り返す。
• 定常状態に達したら、そのデータからランダムにサンプリングする。ここでの樹形の出現頻度が、その樹形の事後確率になるらしい。

系統樹作成の際の一般的注意点

実際に分子系統樹を作成するのはコンピューターなので、とりあえず配列を入れればそれっぽい系統樹を作ることができる。しかし、系統樹作成のアルゴリズムにはいくつかの仮定があり、それらを満たしていない配列を使うと、信頼性の低い系統樹が出来上がってしまう。

> ありがちな間違いが、「系統解析の落とし穴」としてまとめられている (4)。

• それぞれの配列が相同であるという仮定がある。また、「良い」アラインメントが得られていないといけないので、ギャップが多く怪しい部分はトリムするのが良いようだ。
• フレームシフト、逆位などで多数のアミノ酸が一度に変異するイベントは想定していないらしい。データ配列から削除する必要がある。
• 形質間で共通の変異メカニズムを想定。例えば、翻訳領域と非翻訳領域では、変異の入り方が異なるはずである。したがって、これらを同時にデータ配列として含めてはいけない。異なる置換モデルを設定して、別々に解析をしなければならない。
• 時間反転可能モデルでは、系統樹上で塩基、アミノ酸置換頻度がほぼ一定であると仮定している。

文献 4 には、これらの仮定を満たすかどうかの検定も紹介されている。

系統樹の評価

更新予定。とりあえず ResearchGate の議論のページに リンク を張っておく。

References

1. Thompson et al. 2009a. Genomic taxonomy of vibrios. BMC Evol Biol 9, 258.
2. Amazon link: ストライヤー生化学: 使っているのは英語の 6 版ですが、日本語の 7 版を紹介しています。サイドバーの「本紹介・和書」にレビューがあります。
3. Amazon link: これだけは知っておきたい 図解 ジェネティクス: サイドバーの「本紹介・和書」にレビューがあります。
4. 分子系統樹推定の落とし穴と回避法. Link: Last access 2020/10/09.
5. ページ編集に伴い削除
6. 仲田 2006a. Bayes 法 (ベイス法) の原理. Link: Last access 2018/05/17.
7. Root. EBML Phylogenetics Introduction. Link: Last access 2022/08/09.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。