事前検定の是非: t 検定の前に正規性や等分散性を検討すべきか

UB3/statistics/group_comparison/preliminary_test

このページの最終更新日: 2024/09/30

  1. 事前検定の問題
    • 「正規性」は母集団の正規性
    • 等分散性を最初にチェックすべきか？
  2. データの変換
    • データの平方根をとる意味

広告

事前検定の問題

ANOVA などの多重検定にも関係する話であるが、t 検定 を例に考えてみる。

t 検定は、正規分布 normal distribution (図) に従うデータに対する検定である。t 検定の前提条件は、Livingston にまとめられているようである (8I)。母集団が skew していると、type I error のリスクが大きくなる (8I)。

したがって、まず別の検定をかけて正規性を判定し、正規分布しているならば t 検定を行うという手順を踏みたくなる。

この際、考慮すべきポイントは以下の 2 点である。正規性を例に説明しているが、等分散性を事前検定する場合でも全く同じである。

  1. 最初に正規性の検定を行い、確認できたら t 検定。この手順を踏むと、同じデータに対して 2 回統計をかける ことになる。これは 2 重検定であり、基本的に避けるべき。全体の有意水準が 5% に収まらなくなる。
  2. 正規性の検定における 帰無仮説 は、「正規分布する」である (8)。この仮説が棄却できない場合、「正規分布する」として t 検定をすることになるが、この状態は論理的に「正規分布するという仮説を棄却する証拠が不十分である」ということで、「正規分布する」ことを証明してはいない。したがって「正規分布するために t 検定をした」という論理に正当性がない。

この項目では、正規性と等分散性を例に、これらの点を解説する。私は、基本的には事前検定には反対で、最初からノンパラメトリックなテストを行うか、Bonferroni 補正をかけるべきという立場である。


「正規性」は母集団の正規性

本題に入る前に、まず正規性について確認しておく。

しばしば誤解されるが、「正規性」とは母集団の正規性であり、標本集団が正規分布しているかどうかは関係ない (1)。つまり、標本集団が図のような正規分布している母集団に由来するかどうかが問題になる。


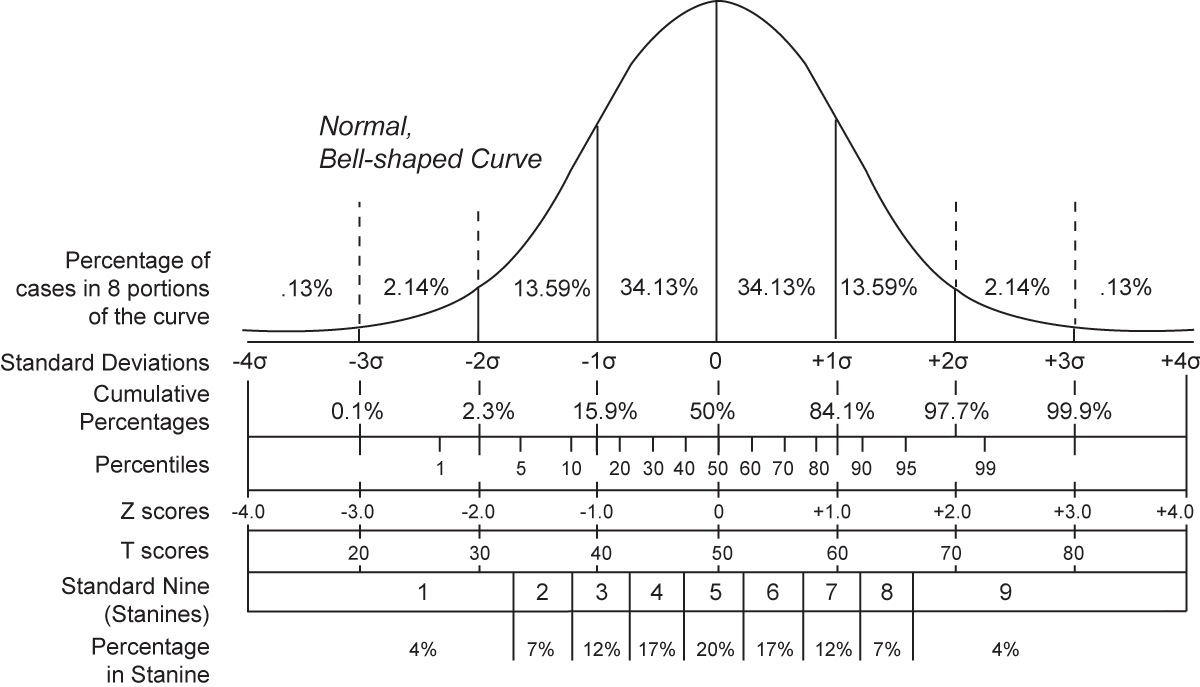
文献 1 には、以下のような専門家のコメントがある。


「たとえば、平均値をt 検定で比べる場合には、動物を何匹か選んできて実験することになるんですけど、その背後にある動物の非常に大きな集団 (母集団といいます) を考えたとき、何かの特性が正規分布しているかどうかが問題で、別に手元にきた100匹とか5 匹の動物 (これをサンプルといいます) が正規分布しているかどうかは問題ではないんです．

「正規分布から選ばれた代表なのかどうかが問題で、もし、背後にある集団で何かの特性が正規分布をしていれば t 検定というのは正確な方法となります．だから、t 検定は近似ではないんです．ただ、背景にある集団が正規分布していないと、必ずしも正確な方法にはなりません．


母集団の正規性を調べる検定としてよく使われるのが、Shapiro-Wilk test である (8)。

母集団の分布を仮定しない方法をノンパラメトリック non-parametric な方法という。検出力 (本当に差があるときに、差があると言える威力) が落ちるが、母集団の正規性が仮定できないときは、t 検定ではなく Mann-Whiteney の U 検定 を行う必要がある。

ただし、正規分布が仮定できなくても、左右対称の分布または対象数が多ければ、多くの場合は t 検定で問題ないというコメントもある (1)。


本題: 事前検定の是非

これも t 検定、等分散の問題を例に説明する。

最初に F 検定で等分散であることを確認し、OK ならば t 検定。この方法には 2 つの問題があった。

1. の問題は、いわゆる多重検定の問題であるので、Bonferroni 補正などを利用して p 値を変更するという対処法もあるようだ (7)。

文献 5 などでは 最初から Welch の検定をする のが良いということになっている。とすると、同じ理屈で最初からノンパラメトリックな検定をしなければならなくなる。

2012 年には「まあ OK じゃないの」という論文もあり (8)、議論の種はつきない問題のようだ。

このページ によくまとまっている。


広告

データの変換

データが正規分布していないときに、平方根などをとることによって正規分布に近づけてから t 検定などをかける場合がある。この項目では、その是非に関する情報を集める。


データの平方根をとる意味

生データではなく、その平方根の値に対して議論している論文がたまにある。これは英語では square root transformation といい、以下のような意味がある。

  • ポアソン分布に従う計数データを square root transform すると、正規分布や Gaussian に近くなる (参考: 確率変数と確率分布 のページに分布の一覧があります)。
  • パーセンテージのデータ、とくに 0 - 20% および 80 - 100% の範囲で有効である (9)。

この ResearchGate のページ では、次のような問題点が指摘されている。一部のみ転載する。

  1. They look at normality of the outcome variable rather than normality of the errors. For OLS models, it is the errors that are assumed to be independently and identically distributed as normal with mean = 0.
  2. They overestimate the importance of the normality assumption. Or putting it another way, they underestimate the robustness of OLS models to non-normality of the errors.

1 についてはよくわからないが、正規性の仮定は、実は outcome ではなく error に適用されると言っているようである。

2 については、正規分布していなくても検定は robust であると言っていて、これは上記の頑健性の話と関係しているだろう。

また、このページ も参考サイトとして挙げられている。

Square root のほか、log および arcsine transformation というのがあるようである。


広告

References

ページ分割のため番号が飛んでいますが、本文と対応しています。

  1. 山中ら 2009a. 分子生物学、生化学、細胞生物学における統計のポイント. 蛋白質核酸酵素 53, 1792-1801.
  1. Welch検定が主流、単純 t 検定や ANOVA は時代遅れ：Statwingの話題から. Link.
  2. Rochon et al. 2012a. To test or not to test: Preliminary assessment of normality when comparing two independent samples. BMC Med Red Method 12, 81.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。

アップデート前、このページには以下のようなコメントを頂いていました。ありがとうございました。

2018/07/20 10:29 このページを拝見して、長年の疑問が解けました。ありがとうございました。


↑