正則化回帰: R によるリッジ回帰とラッソ回帰、解釈など
UB3/statistics/correlation/regression_ridge
このページの最終更新日: 2025/12/15広告
概要: 正則化回帰とは
このページでは、データにノイズを入れて overfitting を回避しつつ、回帰係数が大きくなることに対してペナルティを与える
まずは、それぞれの方法の概念を簡単に。
回帰分析は、説明変数 X によって応答変数 Y の変動を予測しようとする分析である (→ 相関と回帰の違い)。説明変数 X が複数ある場合、重回帰分析 と呼ばれる。
重回帰分析において、それぞれの説明変数 X 同士に相関があると、回帰係数が大きくなり、全体の回帰の信頼性が下がってしまう。これを多重共線性 multicollinearity の問題という。
正則化回帰は、この問題を解決する方法の一つである。モデルに正則化項を加え、過学習を避ける。
リッジ回帰 |
線形回帰に、学習した重み (回帰係数のことのようだ) の二乗の合計を加える (2)。 |
ラッソ回帰 Lasso regression |
線形回帰に、学習した重みを二乗せずに加える (2)。 リッジ回帰とは異なり、説明変数の係数が 0 になる (つまり説明変数が取り除かれる) ことがある。説明変数の選択を自動で行ってくれるとも言える。
|
Elastic net |
リッジ回帰とラッソ回帰の折衷案 (2)。 ラッソ回帰ではモデルに取り込める説明変数の数に制限があるが、この問題点がなくなっているらしい。 |
R を使った正則化回帰
3 つの回帰の方法は極めて似ていて、alpha = 0 ならリッジ回帰、1 なら Lasso 回帰、0 < α < 1 なら elastic net になる。
ここでは、BostonHousing という R の組み込みデータセット を用いて、実際の回帰を行ってみる。参考にしたのは 東京に棲む日々 ほか。最終的なモデルの評価は、このページ のように予測値と実測値のプロットで良いのか?
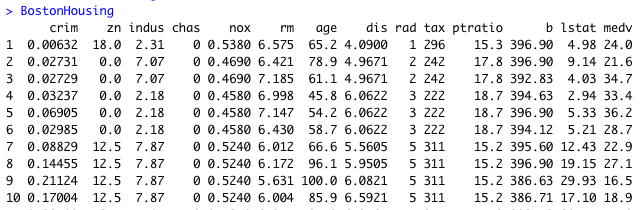
まず、BostonHousing のデータセットである。ボストンの家のデータが 14 項目にわたって収められており、データ数は 506 個である。図には最初の 10 個だけを載せている。一番右にある medv は median value of owner-occupied homes in USD 1000's つまり家の値段であるので、これを応答変数 Y として、残り 13 個の要因がどれだけ Y を予測できるか、正則化回帰で調べてみることにする。
R スクリプトのファイルは ここ からダウンロードできる。
まずは必要なライブラリーとデータをロードする。
data("BostonHousing")
library(glmnet)
library(tidyverse)
library(broom)
次に、BostonHousing の 13 個の要因を説明変数 X、medv を応答変数 Y として保存する。正則化回帰では、説明変数はベクターやデータフレームではなく、行列として読み込む必要がある。
- 正則化回帰は線形回帰であり、応答変数は連続変数である。0 と 1 の二値変数はとらないので注意。R で指定する列が factor になっていると、Error in storage.mode(y) <- "double" : invalid to change the storage mode of a factor というエラーになる。
- この場合は、まず 0 と 1 の列を as.numeric() で数字に変換する。
- 次に、glmnet(predictors, response_binary, alpha = 1, lambda = lambdas, family = "binomial") のように、bimodal を指定する。
- これによって、モデルは LASSO ペナルティ付きの ロジスティック回帰 となる。
chas, nox, rm, age, dis, rad, tax, ptratio, b, lstat) %>% data.matrix()
response_variable = BostonHousing$medv
変数ラムダを指定する。正則化回帰を行う関数は glmnet である。alpha の指定が重要で、alpha = 0 だとリッジ回帰、1 だとラッソ回帰、0 と 1 の間だと弾性ネットになる。
fit = glmnet(predictors, response_variable, alpha = 0, lambda = lambdas)
plot(fit, xvar = "lambda", label = TRUE)
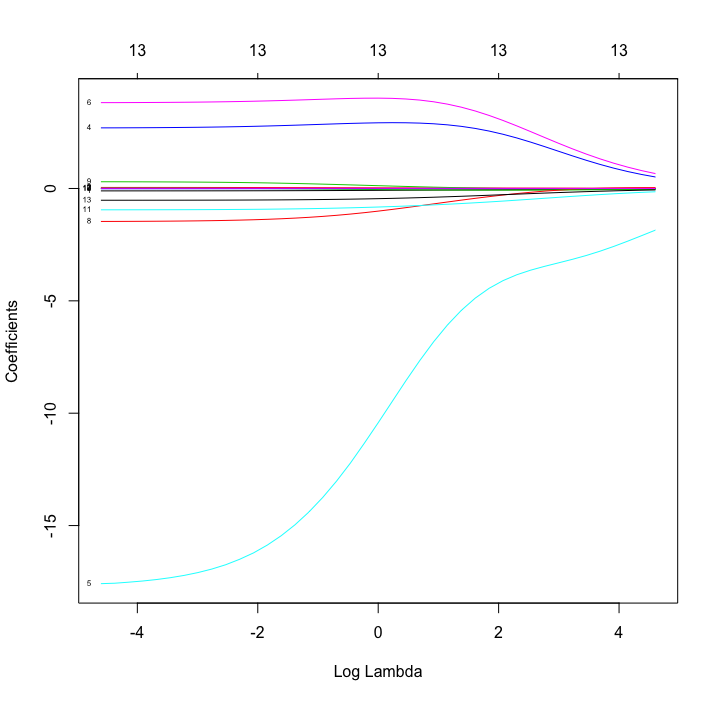
このプロットにより、以下のような図が出力される。横軸は log lambda, 縦軸は回帰係数である。小さくて見にくいが、それぞれの線に番号が降ってある。それぞれの線は指定した X を示し、lamda が大きくなるほど回帰係数が小さくなることがわかる。
この図は alpha = 0 のリッジ回帰。
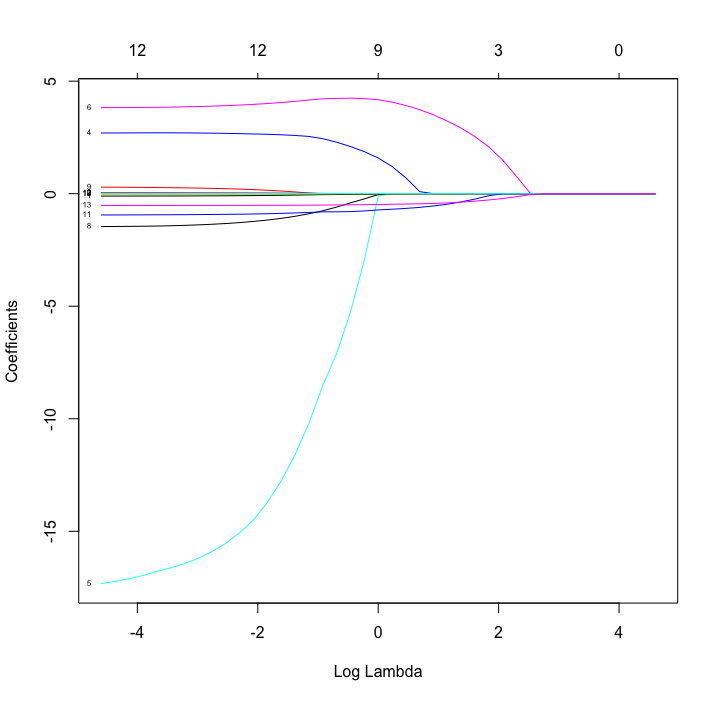
alpha = 0.5 の弾性ネット。リッジ回帰と同様に、回帰係数は lambda が大きくなるほど 0 に近づいていくが、弾性ネットではその収束がリッジよりも早いことがわかる。
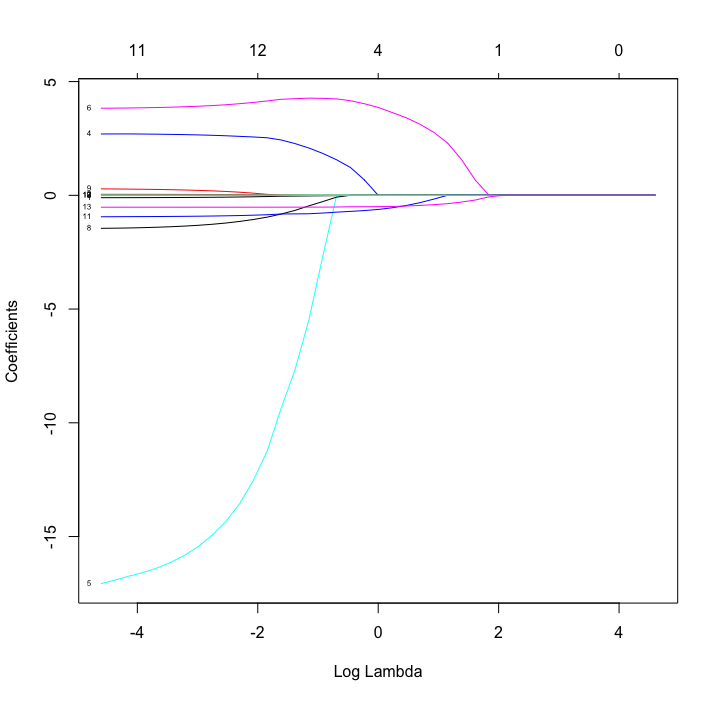
これが alpha = 1 のラッソ回帰。収束は弾性ネットよりもさらに早い。
lambda の値が重要であるので、どの値が最適化をクロスバリデーションで調べる。関数は cv.glmnet である。
lambda_calc = cv.glmnet(predictors, response_variable, alpha = 1, lambda = lambdas, grouped = FALSE)
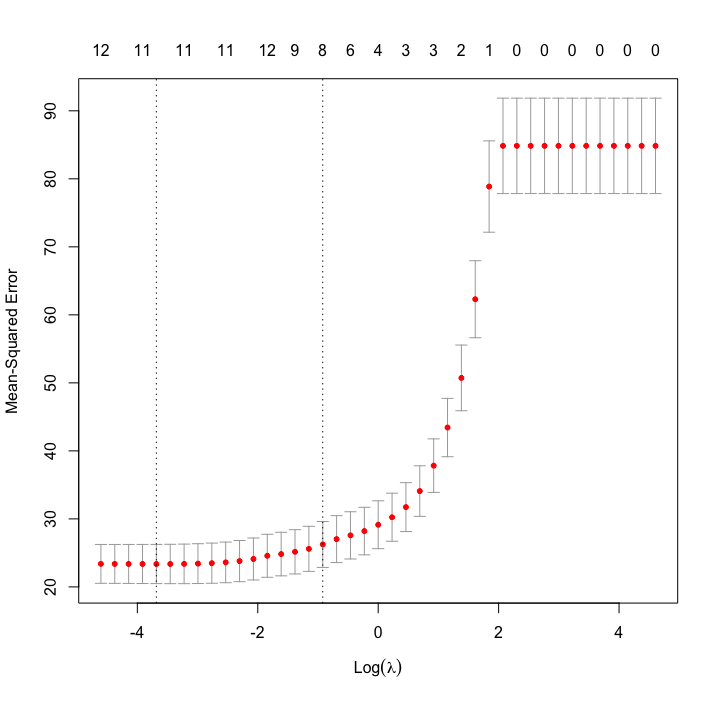
plot(lambda_calc)
optlambda = lambda_calc$lambda.min
ラッソ回帰の場合のプロットのみを示す。縦軸は mean squared error で、左側の線で最小となる。これに対応する lambda が最適な lambda であり、これを optlambda として保存。
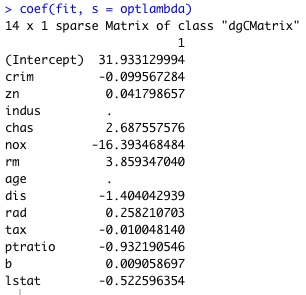
optlambda に対応する回帰係数を表示する。関数は coef である。
まずはラッソ回帰の結果を示す。いくつかの変数は回帰係数が . となっており、回帰と同時に変数の選択が行われていることがわかる。
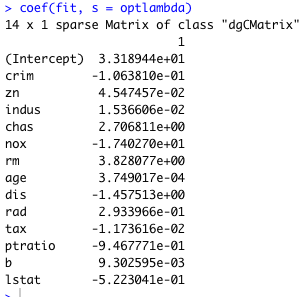
一方、リッジ回帰ではこのように変数が全て残る。
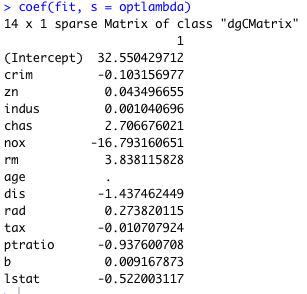
弾性ネットは両方の性質をもつので、変数選択はするがラッソよりも残る数が多い。
多重共線性について
ここも、内容が増えてきたらページ分割することになるだろう。
多重共線性 multicollinearity とは、多重線形回帰に用いる説明変数 X の間に相関があることによって生じる問題である。強いものと弱いものがあり、このサイト では説明変数間の線形相関が強く、そもそも解が求まらない状況を「強い多重共線性」、線形相関が弱く解は求まるが、推定結果が不安定になる状況を「弱い多重共線性」としている。
多重共線性にもいろいろ種類があるようで (3)、その影響も推定結果がおかしくなる、推定結果の分散が大きくなる、そもそも解が求まらないなど、結果も多様なようである。
多重共線性のチェック方法
- 説明変数同士の相関を見る。ただし、多重共線性は説明変数同士にシンプルな相関 (X1 = a + bX2) があるときに生じる可能性があるが、実はそれだけではなく、複数の説明変数同士で多重回帰のように X1 = aX2 + bX3 + c のような関係が成り立つときにも生じる (3)。したがって、シンプルに相関係数同士を plot するだけでは不十分。
統計と機械学習の枠組みで違いが生じるようである。統計と機械学習の違いについて。
正則化回帰を使っても、やはりサンプル数が少ないと良い回帰はできない (参考)。とくに、説明変数が dense (多くの説明因子が少しずつ寄与している) な場合、lasso のパフォーマンスは非常に悪くなる。Ridge, random forest のがまだマシ。一方、説明変数が sparse (強く影響する少数の因子がある) なときは、lasso のパフォーマンスが良くなるようだ。
広告
References
- 罰則付き・正則化回帰モデルについて. Link: Last access 2020/06/08.
- 超入門!リッジ回帰・Lasso回帰・Elastic Netの基本と特徴をサクッと理解! Link: Last access 2020/06/08.
- 多重共線性とは~回避の方法として相関を見るだけでは..... バナナでもわかる話. Link: Last access 2020/06/26.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
