最小二乗法による線形回帰: 原理、注意点など
UB3/statistics/correlation/regression_ols
このページの最終更新日: 2025/11/23このページでは、線形回帰と最小二乗法の原理や、適用する際に考えるべき点についてまとめる。実際の分析は、R lm 関数を用いた回帰分析 のページに移動した。
- 概要: 線形回帰とは
- 最小二乗法とは
- 線形回帰の実際
- カテゴリー化
- 対数変換
- 因果推論
広告
概要: 線形回帰とは
相関と回帰の違い のページで述べたように、回帰とは
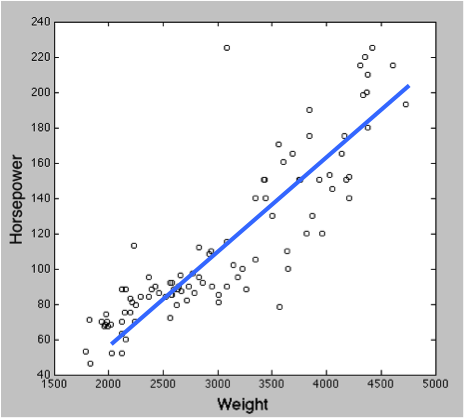
- 通常は、変数 x によって変数 y の変化を予測することになる。x が一つならば単回帰分析、複数ならば重回帰分析である。
- 青い直線を示す式が x と y の関係性を表すことになる。
x と y はさまざまな名前で呼ばれる。
x は独立変数 independent variable のほか、説明変数 explanatory variable、予測変数 predictor variable とも呼ばれる。連続変数であることが一般的だが、名義尺度 しか持たないカテゴリー変数でも OK。
y は応答変数 response variable (目的変数、反応変数) という名前のほか、従属変数 dependent variable、基準変数 criterion variable、非説明変数 explained variable とも呼ばれる。
最小二乗法とは
線形回帰では、x と y の関係を示す直線が使われる。「データを fit させる」という。上の図の青い線であり、この直線は
- 全てのデータポイントが直線上に乗っていれば、話は単純である。全ての点を通る直線が回帰直線となり、y は x によって 100% 予測可能であるということになる。
- しかし実際にそうなることはほとんどなく、観測値がばらつく。そこで、
全てのデータにできるだけ近い線 が回帰直線ということになる。
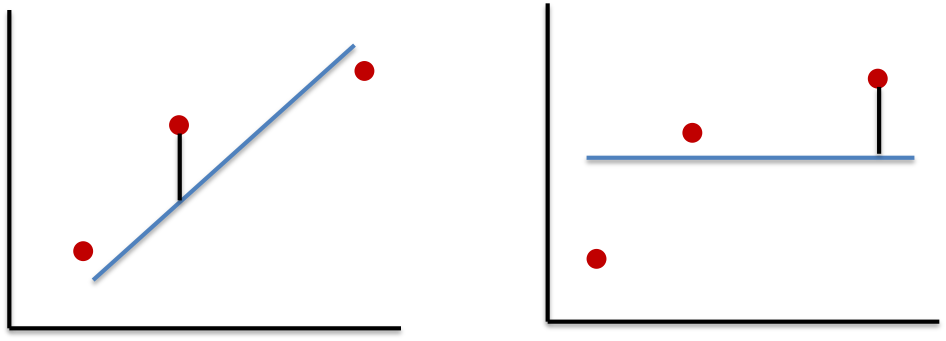
最小二乗法のポイントは、回帰直線とデータの差 (誤差) を
線形回帰には、回帰モデルへの適合度を示す 決定計数 という数値がある。
また、その回帰が有意であるかどうかを判定することも可能である。この場合、帰無仮説は「勾配が 0 に等しいため、y と x の間には定量的な依存関係がない」になる。
線形多重回帰 の方法も、これに極めて近い。
広告
線形回帰の実際
実際に線形回帰を行う際、考えるべきポイントについて。
カテゴリー化
体重、身長、BMI などの連続変数を回帰分析に入れるとき、そのまま数値変数として右辺に入れたくなるが、これは
対数変換
線形回帰の基本は y = ax + b であるが、実際には変数 x および y の対数を用いて、以下のような式で回帰している場合が多い。
logey = A * logex + b
> 回帰分析における対数変換の意味について解説したページ (1,2)。
- 対数変換をすると、異なるモデルにフィットすることになるので、回帰の結果が変わる。「両方を対数にしているから同じ」ということにはならない。
- すなわち、y = ax + b には「a が一定」という前提があり、logey = A * logex + b には「A が一定」という前提がある。
- 両方の式を a および A について解くと、a = (y-b)/x であるが、A = (dy/y)/(dx/x) であり、両者はもちろん異なるものである。A は「弾力性」と言われる。
広告
References
- 対数変換を行う意味について。回帰分析において対数変換する背景にある前提とは? Link: Last access 2020/06/01.
- 一般化線形モデル. Link: Last access 2020/06/08.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
