1. 概要: モンティ・ホール問題とは
2. モンティ・ホール問題の解法・考え方 (1)
   • 扉を変えない場合は 1/3
   • 扉を変える場合は 3 パターンある
3. モンティ・ホール問題の解法・考え方 (2)

概要: モンティ・ホール問題とは

一般の小説でも取りあげられるようになった有名な確率問題。貴志雄介「悪の教典」 (Amazon link) から引用してみよう。

この問題は有名なので、ネット上にも様々な考え方の解法が載っている。一番わかりやすいと思った説明を一つだけ紹介しておく。英語版の Wikipedia にあった説明だ。本来、この問題では賞品が車で、外れのドアの向こうにはヤギがいるので、説明にはそのような図が使われている (Public domain)。

モンティ・ホール問題の解法・考え方 (1)

扉を変えない場合は 1/3

まず、最初に選んだ扉を変えない場合。これは簡単で、司会者が何をしようと確率は 1/3 である。

扉を変える場合は 3 パターンある

次に、扉を変える場合を考えてみる。これは 3 つのパターンに分けることができる。それぞれの場合の確率を足し合わせて、1/3 以上になれば「変える方が良い」と言える。

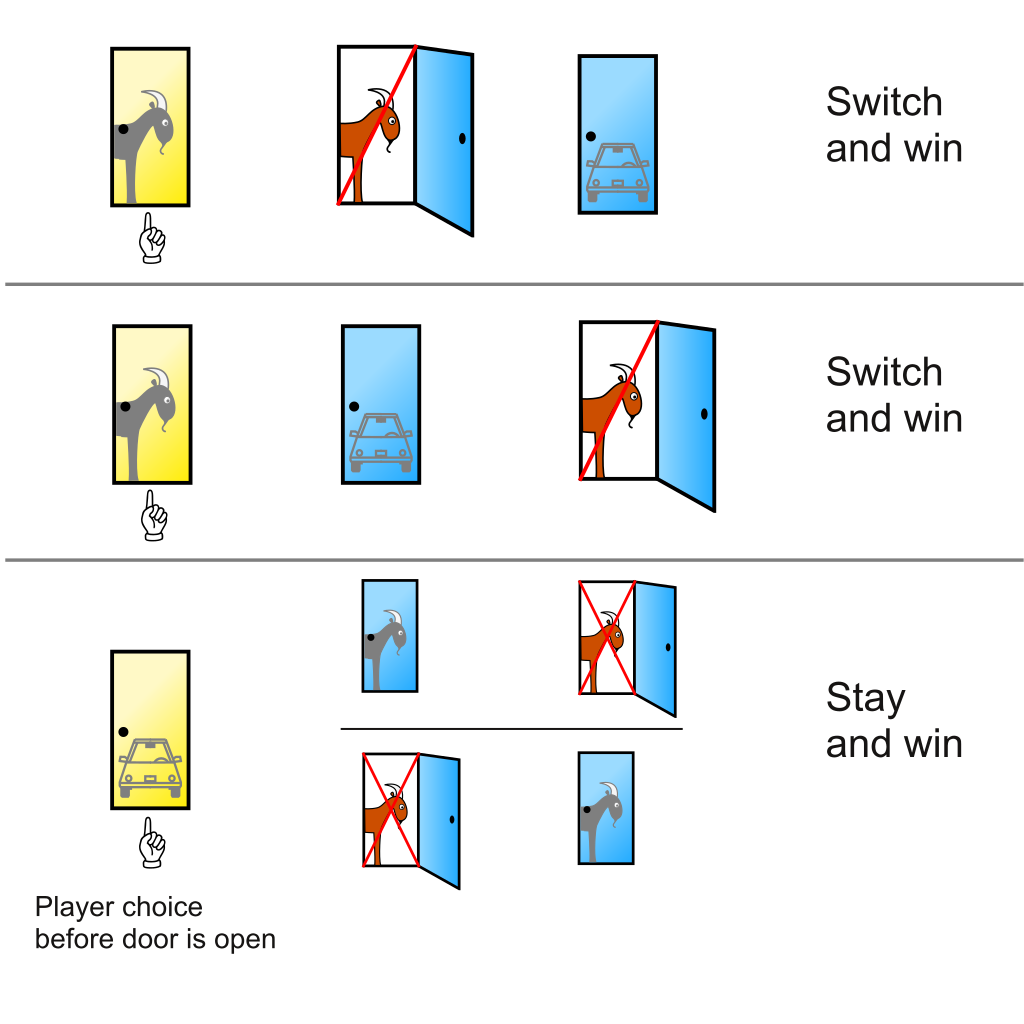
パターン 1

上の図 (Public domain) の一番上に相当する。

最初にハズレの扉 A を選ぶ。この場合は「扉を変える」ことが前提なので、青い扉にスイッチしなければならない。

2 つある青い扉のうち 1 つは、司会者によって既にハズレであることが示されている。したがって、扉を変えることによって確実に車をゲットできることになる。

最初に「この」ハズレの扉を選ぶ確率は 1/3 で、扉を変えることによって車を当てられる確率は 1 である。したがって、このパターンでの全体としての確率は 1/3 x 1 = 1/3 となる。

パターン 2

最初にもう一つの外れの扉 B を選んだ場合にも全く同様の結果になる。扉を変えると確実にゲットできるので、この確率も 1/3 である。

パターン 3

最初に車が入っている扉 C を選んだ場合、扉を変えてしまうと車は手に入らない。図では車と指マークが右端にあると思ってほしい。したがって確率は 0 である。

以上を合計すると、扉を変えたときに車をゲットできる確率は、1/3 + 1/3 + 0 = 2/3 となり、扉を変えなかった場合の 2 倍 となることがわかる。

モンティ・ホール問題の解法・考え方 (2)

上と似ているが、このような樹形図 (Public domain) を使う考え方もある。

この図は、最初に扉 1 を選んだ際 の場合分けである。

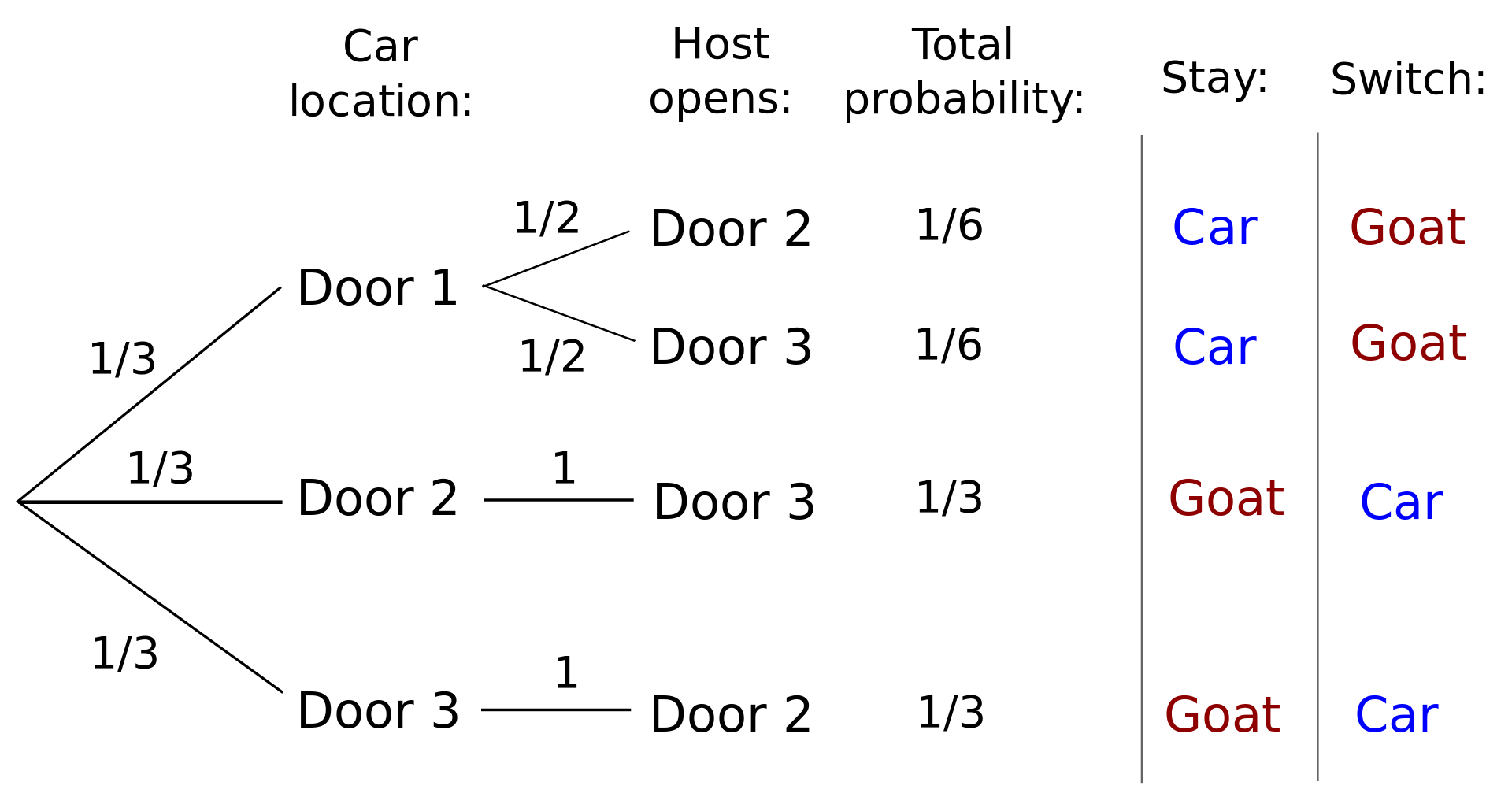
車が他の扉 (Door 2 と Door 3) に入っている場合、上の説明と同様に、stay すると車は得られず、switch すると確実に得ることができる。

車が Door 2 と Door 3 にある確率はそもそも 1/3 ずつなので、switch した場合は合計して 2/3 の確率となる。

一方、車が Door 1 にある場合、stay することで車を得られる。その確率は 1/3 となる。

References

1. 確率と確率変数. Web pdf.
2. 貴志祐介 2010a. 悪の教典. 文芸春秋.

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。