算術平均、幾何平均、中央値、最頻値の意味、違い、使い方

このページの最終更新日: 2024/09/30

概要: 記述統計について

統計は、大きく記述統計 descriptive statistics と、推測統計 inferential statistics に分類される。記述統計には母集団・標本集団という概念がなく、集団の特徴をどのように要約するかが主眼となる。

このページでは、集団の要約に使われる平均値、中央値、最頻値などの意味と、その使い方をまとめる。ただし、これらの値は記述統計のみで使われるものではなく、推測統計でも重要である。

算術平均 arithmetic mean は、相加平均とも呼ばれ、一般に使われている「平均」である。つまり変量の総和を変量の個数で割ったもので、以下の式で与えられる。

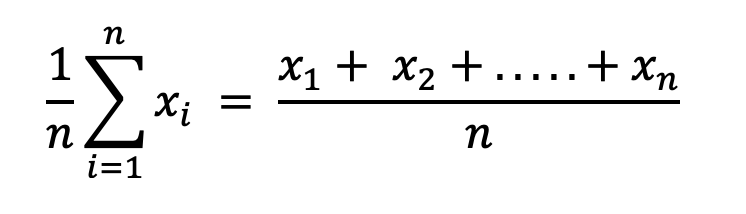
単に平均値 mean と言った場合、普通はこの算術平均を意味する。外れ値に敏感であるという特徴があり (4)、外れ値のあるような分布では使用に注意が必要である。

幾何平均 geometric mean は、相乗平均とも呼ばれ、幾何平均の足し算を掛け算にしたもの。つまり n 個の各変量をすべて掛け合わせて、その n 乗平方根をとる。

例えば、企業の売り上げが今年は 3% アップ、昨年は 5% アップであった場合に、平均して何%アップしたかを計算したい場合は、算術平均でなく幾何平均をとる (2)。つまり、掛け合わせることに意味のある値の平均を計算する場合は、幾何平均が適している。

Fundamentals of Biostatistics では、データがべき乗で表されるときに幾何平均が有効とされている。しかし、値をそのまま扱うのではなく、対数をとることが推奨されている。

中央値 median (より正確には標本中央値 sample median) は、変量を小さい順に並べたとき、分布の中央に来る値である。変量の個数が奇数のときは中央の値を、偶数のときは中央にある 2 つの値の算術平均をとって中央値とする。

1 2 3 4 5 → 3 が中央値

1 2 3 4 5 6 → 3.5 が中央値

> 数式を使って定義すると、次のようになる (4)。

その定義上、中央値は順番でのみ定義される。つまり、実際のデータが 1 2 3 4 5 でも 1 2 3 99 100 でも中央値は 3 になる。したがって、この 99 100 という数値の大きさが意味をもつような分析では、中央値の使用に注意が必要である。

最頻値 mode は、最も頻度の多い値である。ヒストグラムが描けるなら、一番高い部分にあたる。

平均値、中央値を計算する際には、それぞれの変数を足しあわせたり、小さい順に並べたりする必要がある。したがって、それぞれ間隔尺度以上または順序尺度以上の尺度水準でなければならない (参考: 尺度水準のページ)。一方、最頻値はカテゴリー変数でも算出することが可能で、これがメリットである。

具体的には、10 人のクラスの成績を A, B, C, D でつけたとき、A B A B B C B C B D になったとする。これらはカテゴリー変数なので平均値、中央値を算出することはできないが、B が一番多く最頻値である。

最頻値には、たくさんありすぎると意味がないという問題点がある (4)。

分布によっては、複数の最頻値が含まれる場合がある (4)。ヒストグラムが山の峰のように見えるので、そのような分布を多峰性 (たほうせい; 英語では multimodal で、mode という言葉が含まれている) の分布という。これに対して、峰が一つだけある分布は単峰性 unimodal という。

二峰性 bimodal の分布 (Public domain)。

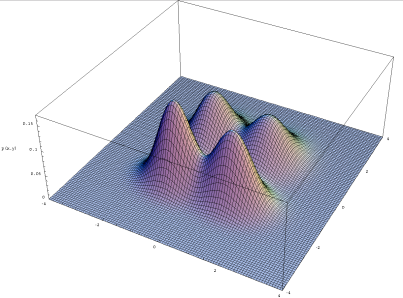
二次元の多峰性分布の一例 (Public comain)。もちろん、一次元で山が複数あっても多峰性分布である。

最頻値が 100 個あるような分布を想像してみよう。分布はだら〜っと一様に広がっており、個々の最頻値にはほとんど意味がないだろう。最頻値は集団に何個でも存在できるが、数が多くなると意味がなくなってくるのである。

平均値、中央値、最頻値は、集団が正規分布をしている場合には全て等しくなる。これらの違いが重要となってくるのは、集団の分布が skew している場合である。

まずは図 (1) の実線を見てみよう。ほぼ正規分布に近い分布であるが、右側に少し tail がある。そのため、median は最頻値から少し右にずれており、mean はさらに右にある。

点線の分布は右側の tail がさらに長く、それぞれの値の違いが大きくなっている。

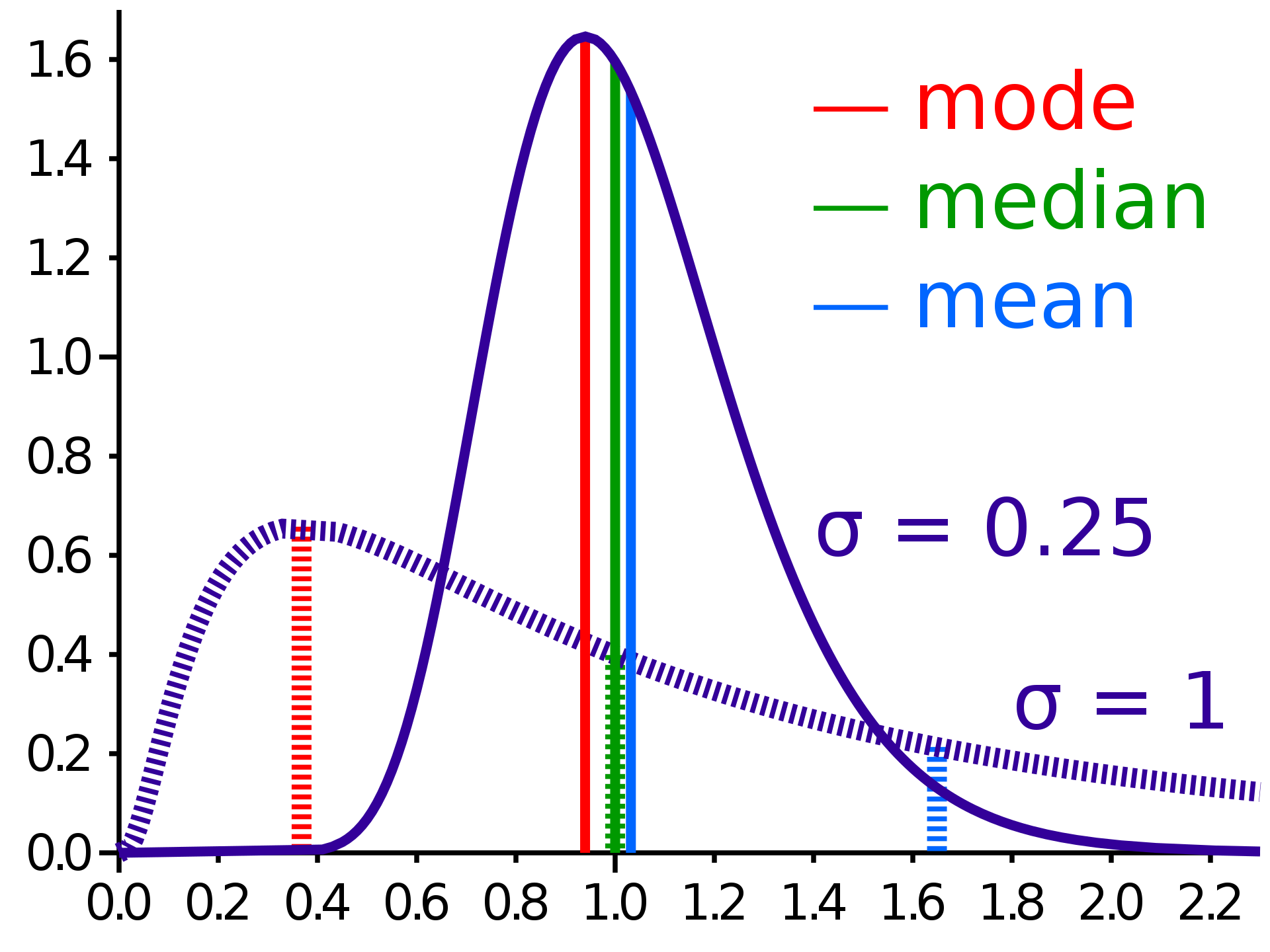
逆に、mean と median の比から分布が skew しているかどうかを推定することも可能である。

平均値や中央値から始まり、t 検定、ANOVA、回帰分析まで、普通の論文で使う統計手法を網羅している本。とにかくグラフ付きの実例が多く、さらにその実例は論文からとられているので、実践的な生物統計を学びたい人にはおすすめの一冊。

統計の本はとっつきにくいものが多いが、2016 年と比較的最近の本であることも特徴だ。著者はハーバード公衆衛生の Bernard Rosner。経歴を見ると医学統計のエキスパートだが、この本はシグマ記号の意味が実例つきで紹介されていることからも分かる通り、平易な解説になっている。

たぶん高校の上級から大学の学部生あたりが基本的なターゲットで、研究に使う際に統計の基礎をチェックしたい研究者にも適した本になっている。

リンク

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。