R: lm 関数による単回帰分析
UB3/informatics/r/regression_lm
このページの最終更新日: 2025/11/23広告
R による回帰分析
回帰とは、
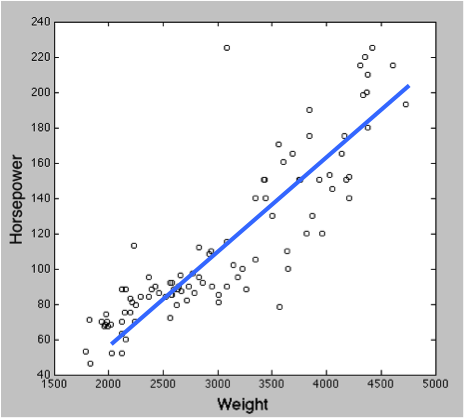
R では、回帰に以下のような基本関数が用意されている。
lsfit |
最小二乗法による回帰 |
lm |
線形モデルによる回帰 |
glm |
一般線形モデルによる回帰 |
nls |
Nonlinear least squares の略。関数を定義して非線形の回帰を行う場合に使う (参考ページ)。最小二乗法を使っている。 |
lm_robust |
分散が不均一な状況でも、頑健な標準誤差が計算できるらしい。estimatr::lm_robust() という形で使う。Twitter でちらっと見ただけの情報なので、いずれ調べて更新。 |
このページでは、R の lm 関数を用いた回帰の方法を説明する。以下のような関連ページもあるので参照のこと。
広告
「あとがき」で当サイトを参考にしたと書いてくれているラノベです。Kindle Unlimited で読めました。ストーリーと文章が良く、面白かったです。
lm 関数の使い方
R の組み込みデータセット swiss を使ってみよう。このデータはピアソンの相関のページで使っており、以下のように Education と Examination というパラメーターに有意な正の相関があることがわかっている。Education は 正規分布 しているとは言えないが、Examination は Shapiro-Wilk 検定で正規分布することが確認されている。
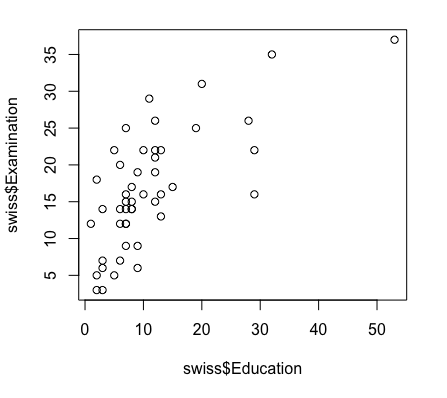
このデータで、Examination つまり試験の成績が、教育 Education によってどの程度予測できるかを回帰分析してみる。
lm を使って回帰の結果を見るには、以下のような手順をとる。
- lm の結果をオブジェクトとして保存する。lm の基本形は
lm(y ~ x) 、つまり lm(従属変数 ~ 説明変数) である。 - または
lm(従属変数 ~. data = 解析するデータフレーム) の形も可能。~ のあとのドット ~. は、「データフレームに含まれる全ての説明変数を考慮する」の意味。 - そのオブジェクトの詳細を summary 関数で表示する。
summary(reg1)
これは、lm の結果を reg1 というオブジェクトに保存し、その summary を見るということ。結果は次のようになる。

この結果で重要なパラメーターは以下の 3 つである。Intercept と 傾き swiss$Education を合わせて Coefficient という。
切片 |
10.12748 となっている。回帰直線 y = ax + b の b、すなわち切片である。 切片の隣に P 値がある。この回帰では P 値が非常に小さいので、有意であると言える。 |
傾き |
切片の下にある swiss$Education の Estimate 0.57947 が回帰直線の傾き。これも有意。 |
決定係数 R2 |
Multiple R-squared および Adjusted R-squared がある。ここでは、Adjusted R-squared 0.4764 が重要である。 これは「y の 47% が x によって説明される」という意味になり、さらに R2 の P 値が非常に小さいので、この回帰は有意であることになる。 |
以上を総合すると、この線形回帰は y = 0.57947x + 10.12748 という式で表され、これが試験の成績 (35 点満点? 両変数の単位はよくわからない) の 47% を説明できると結論できる。
lm 関数のアウトプット
上記のように、lm 関数の結果 reg1 に対して summary 関数を使うと、サマリー情報を見ることができる。「普通に」統計検定をかけるだけなら summary の情報で十分であるが、状況によっては reg1 の情報を他の関数に受け渡して、さらに解析を進めなければならないような場合もある。
lm 関数のアウトプットについて、少し詳しく見てみよう。View(reg1) とする。
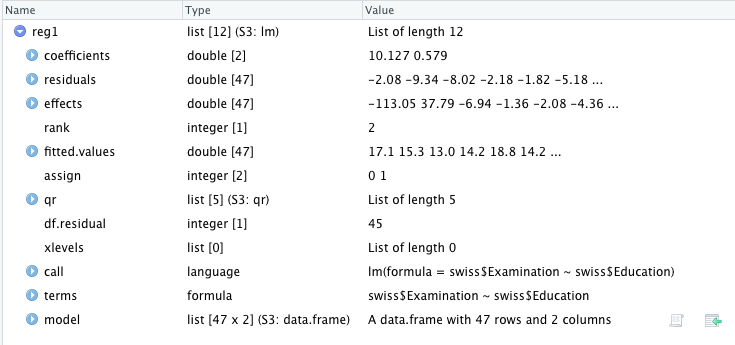
reg1 は、12 個の項目が含まれる list というデータ形式である。
Coefficient には数値が 2 つある。10.127 と 0.579 である。上記の summary の部分をみればわかるように、10.127 は切片、0.579 が傾きになる。ゆえに、この回帰式は y = 0.579x + 10.127 ということになる。
広告
References
- 71. 回帰分析と重回帰分析. Link: Last access 2020/05/28.
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
