Matlab: corr 関数

UB3/informatics/commands_matlab/corr_matlab

このページの最終更新日: 2024/09/30

  1. corr の基礎: corr(x), corr(x,y)
  2. 統計検定: [r,p] = corr(x) という使い方

広告

corr の基礎: corr(x), corr(x,y)

これは、MATLAB help では RHO = corr(x) の形で説明されている。RHO はギリシャ文字のロー ρ であり、相関係数を意味する。決定係数 coefficient of determination, r2 とは異なるので注意すること。

また、要素のなかに 1 つでも NaN が含まれていると、その列から計算される相関係数および p 値も全て NaN になってしまう。この場合は、isnanで NaN を取り除く必要がある。

行列の中での相関

a が m 行 n 列の行列のとき、corr(a) はそれぞれの列ごとに総当たりで相関係数 pairwise linear correlation coefficient を計算し、 n x n の行列として結果を返す。

>> a=rand(7,3)
a =
0.2564 0.1357 0.4132
0.9706 0.7852 0.2457
0.2041 0.6642 0.8822
0.9053 0.7312 0.6948
0.1613 0.1758 0.6801
0.4713 0.3685 0.0310
0.9373 0.7082 0.6467

>> corr(a)

ans =
1.0000 0.7655 -0.1850
0.7655 1.0000 0.2024
-0.1850 0.2024 1.0000

この結果は、a の 1 列目（0.2564, 0.9706...)と 2 列目の相関係数が 0.7655 というように見る。ans の対角線上に 1 が並んでいるのは、a の 1 列目と a の 1 列目、a の 2 列目と a の 2 列目...の相関係数が 1 だからである。

2 つのベクター間の相関

上の行列の 1 列をベクターとして、以下のように相関係数を計算することができる。

>> b=a(:,1);
>> c=a(:,2);
>> corr(b,c)

ans = 0.7655

2 つの行列間の相関

組み合わせが多いのでややこしいが、総当たりの計算結果がどのように表示されるかというだけの問題である。 MATLAB の解説ページ (1) の通りに、30 x 4 の行列 x, y を作り、その相関を調べてみる。

なお、ここではある程度の相関があるように x, y を設定している。


>> x
x =
    0.5377    0.8884   -1.0891   -1.1480
    1.8339   -1.1471    0.0326    0.1049
   -2.2588   -1.0689    0.5525    0.7223
    0.8622   -0.8095    1.1006    2.5855
    0.3188   -2.9443    1.5442   -0.6669
   -1.3077    1.4384    0.0859    0.1873
   -0.4336    0.3252   -1.4916   -0.0825
    0.3426   -0.7549   -0.7423   -1.9330
    3.5784    1.3703   -1.0616   -0.4390
    2.7694   -1.7115    2.3505   -1.7947
   -1.3499   -0.1022   -0.6156    0.8404
    3.0349   -0.2414    0.7481   -0.8880
    0.7254    0.3192   -0.1924    0.1001
   -0.0631    0.3129    0.8886   -0.5445
    0.7147   -0.8649   -0.7648    0.3035
   -0.2050   -0.0301   -1.4023   -0.6003
   -0.1241   -0.1649   -1.4224    0.4900
    1.4897    0.6277    0.4882    0.7394
    1.4090    1.0933   -0.1774    1.7119
    1.4172    1.1093   -0.1961   -0.1941
    0.6715   -0.8637    1.4193   -2.1384
   -1.2075    0.0774    0.2916   -0.8396
    0.7172   -1.2141    0.1978    1.3546
    1.6302   -1.1135    1.5877   -1.0722
    0.4889   -0.0068   -0.8045    0.9610
    1.0347    1.5326    0.6966    0.1240
    0.7269   -0.7697    0.8351    1.4367
   -0.3034    0.3714   -0.2437   -1.9609
    0.2939   -0.2256    0.2157   -0.1977
   -0.7873    1.1174   -1.1658   -1.2078
 		>> y
y =
    2.9080    0.5201   -1.3617   -0.8110
    0.8252   -0.0200    0.4550    0.8242
    1.3790   -0.0348   -0.8487   -2.0529
   -1.0582   -0.7982   -0.3349    3.7388
   -0.4686    1.0187    0.5528   -1.7482
   -0.2725   -0.1332    1.0391    0.4040
    1.0984   -0.7145   -1.1176   -1.6825
   -0.2779    1.3514    1.2607   -3.0876
    0.7015   -0.2248    0.6601    3.4481
   -2.0518   -0.5890   -0.0679    1.6137
   -0.3538   -0.2938   -0.1952   -1.2274
   -0.8236   -0.8479   -0.2176    2.6535
   -1.5771   -1.1201   -0.3031    0.9523
    0.5080    2.5260    0.0230    0.5939
    0.2820    1.6555    0.0513   -0.6115
    0.0335    0.3075    0.8261   -2.2376
   -1.3337   -1.2571    1.5270   -1.2214
    1.1275   -0.8655    0.4669    3.3450
    0.3502   -0.1765   -0.2097    4.0368
   -0.2991    0.7914    0.6252    2.1363
    0.0229   -1.3320    0.1832   -0.9112
   -0.2620   -2.3299   -1.0298   -1.6781
   -1.7502   -1.4491    0.9492    1.0555
   -0.2857    0.3335    0.3071    1.0323
   -0.8314    0.3914    0.1352    0.6385
   -0.9792    0.4517    0.5152    3.3880
   -1.1564   -0.1303    0.2614    2.2290
   -0.5336    0.1837   -0.9415   -2.1367
   -2.0026   -0.4762   -0.1623    0.0863
    0.9642    0.8620   -0.1461   -2.0436

>> corr(x,y)

ans =
  -0.1686   -0.0363    0.2278   0.6901
   0.3022    0.0332   -0.0866   0.2617
  -0.3632   -0.0987   -0.0200   0.3504
  -0.1365   -0.1804    0.0853   0.4908

となる。ここで、たとえば左上の -0.1686 は、x の 1 列目 と y の 1 列目の相関係数である。まとめて図示すると

ans =
  x(:,1) vs. y(:,1)   x(:,1) vs. y(:,2)    x(:,1) vs. y(:,3)   x(:,1) vs. y(:,4)
  x(:,2) vs. y(:,1)   x(:,2) vs. y(:,2)    x(:,2) vs. y(:,3)   x(:,2) vs. y(:,4)
  x(:,3) vs. y(:,1)   x(:,3) vs. y(:,2)    x(:,3) vs. y(:,3)   x(:,3) vs. y(:,4)
  x(:,4) vs. y(:,1)   x(:,4) vs. y(:,2)    x(:,4) vs. y(:,3)   x(:,4) vs. y(:,4)

のようになる。


[r, p]=corr(x,y) という使い方

相関 correlation には、相関係数の大小の他に、2 変数が有意に相関しているかどうか という概念がある。以下のコマンドで、変数 X と変数 Y の相関についての p 値が上と同じ配置で表示される。

>> [rho,pval]=corr (X,Y)

MATLAB のサンプルデータを使って試してみる。以下のコードで図が出力され、ρ = 0.8471 と p = 1.1821e-28 がコマンドラインに表示される。

clear all;
load carsmall; % Load sample data
fs=18;
plot(Weight,Horsepower,'ko');
xlabel('Weight','fontsize',fs);
ylabel('Horsepower','fontsize',fs);
Horsepower(isnan(Horsepower))=0;
[rho,pval]=corr(Horsepower,Weight)

相関

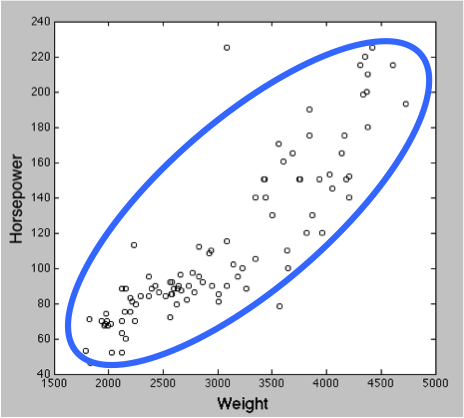
carsmall は 加速度 acceleration, 馬力 horsepower, 重量 weight などを含む MATLAB のサンプルデータである。ここでは、最も相関のありそうな馬力と重量をプロットした。ただし、Horsepower のデータには欠損値 NaN が含まれているので、isnan を使ってこれを取り除いてから相関分析を行っている。

負の相関 についても見てみよう。同じデータセットで、馬力と燃費 (MPG, mile per gallon というアメリカのガソリン消費量の単位) のプロットは右のようになる。

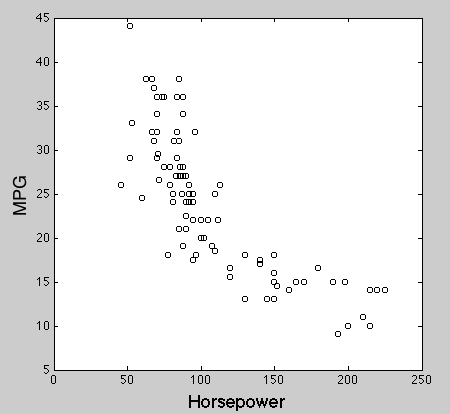
ρ = -0.7440, p = 7.4333e-19 で、ρ が負になるという負の相関がみられ、この相関は有意である。

相関

広告

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。


↑